[机械原理][Python]平面连杆机构的运动分析

PDF文章下载（严禁将本文章包括但不限于用于作弊、抄袭的用途上，欢迎指出问题！）：http://pan.baidu.com/s/1hqxRhju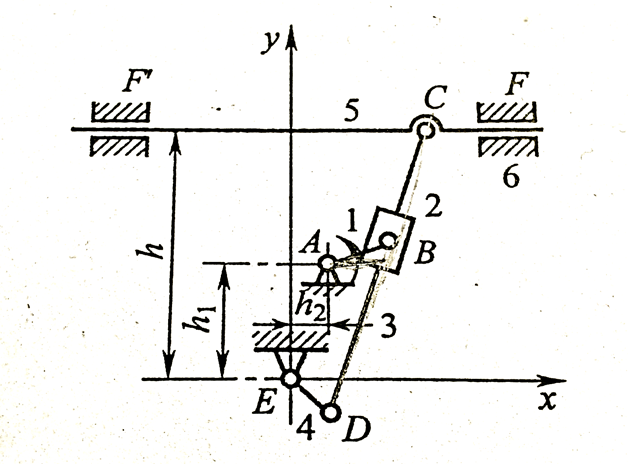
如图所示为一个牛头刨床（III级机构），假设各个构件尺寸如图表所示，原动件1以等角速度ω=1 rad/s沿逆时针方向回转，试求各从动件的角位移，角速度以及角加速度以及刨头C点的位移、速度以及角加速度的变化情况。

首先，我们由AEDB和EDC的两个四边形中，获得几何关系(由于本弱还不知道怎么往网页里面插入Latex，所以只能拿Source Code Pro来凑数了)

l4coso4 + s3coso3 = h2 + l1*coso1

l4sino4 + s3sino3 = h1 + l1*sino1

l4coso4 + l3coso3 – s5 = 0

l4sino4 + l3sino3 = h

直接使用最小二次迭代法求出o3,o4,s5,s3

由于此时求出了o3,o4,s5,s3，对上面这个方程求导即可

2.速度求解：

-l4sino4w4 + s3’coso3 – s3sino3w3 = -l1sino1*w1

l4coso4w4 + s3’sino3 + s3coso3w3 = l1coso1*w1

-l4sino4w4 – l3sino3w3 – s5’ = 0

l4coso4w4 + l3coso3w3 = 0

给出矩阵式：

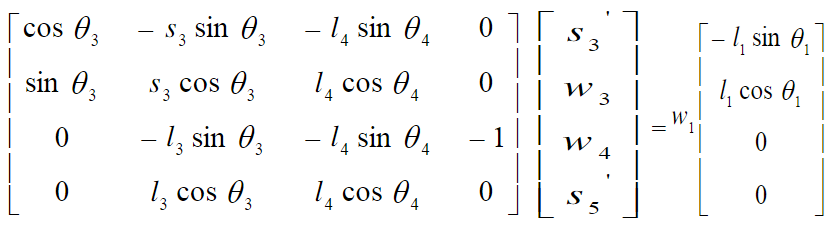
利用高斯消元（解线性方程组）可以得到角速度w3，w4

3.加速度求解

继续对线性方程组进行微分可得：

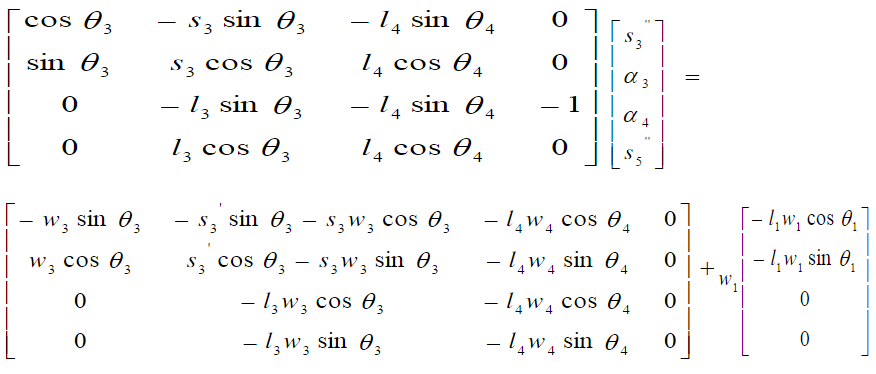
角加速度a3和a4就被解出来了

下面附上第一组的python解法…

机构的位置：

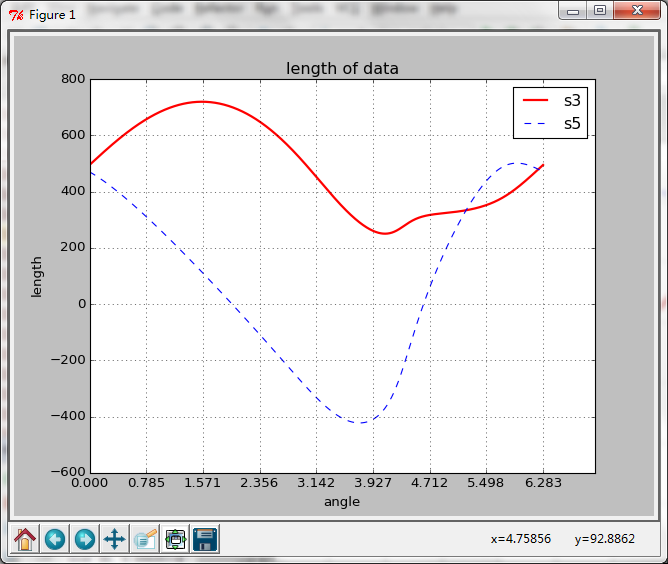
速度的解：

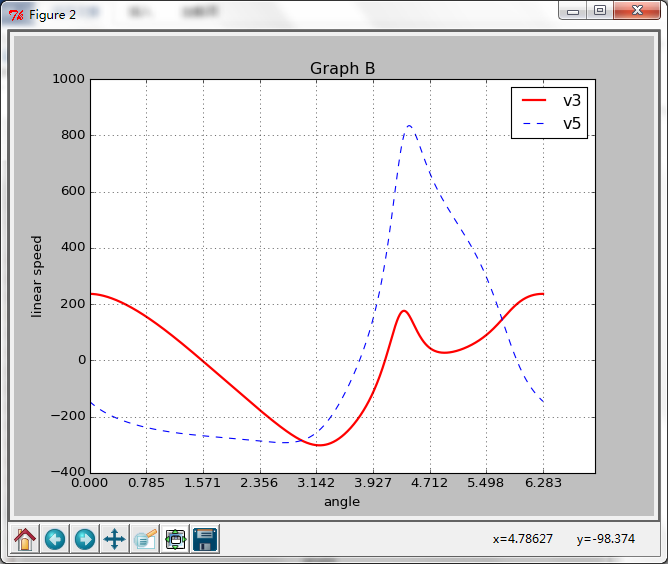
角速度的解

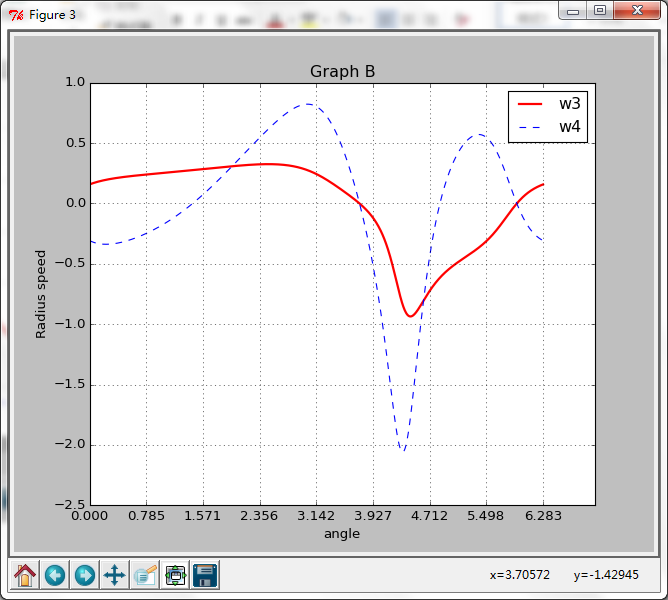
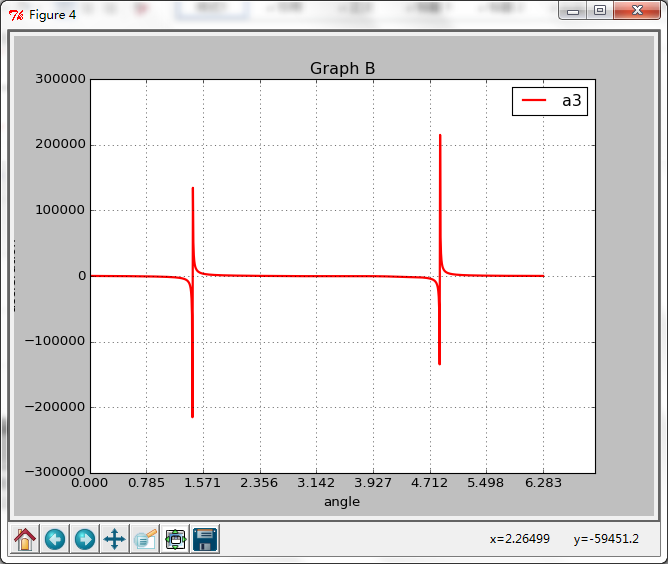
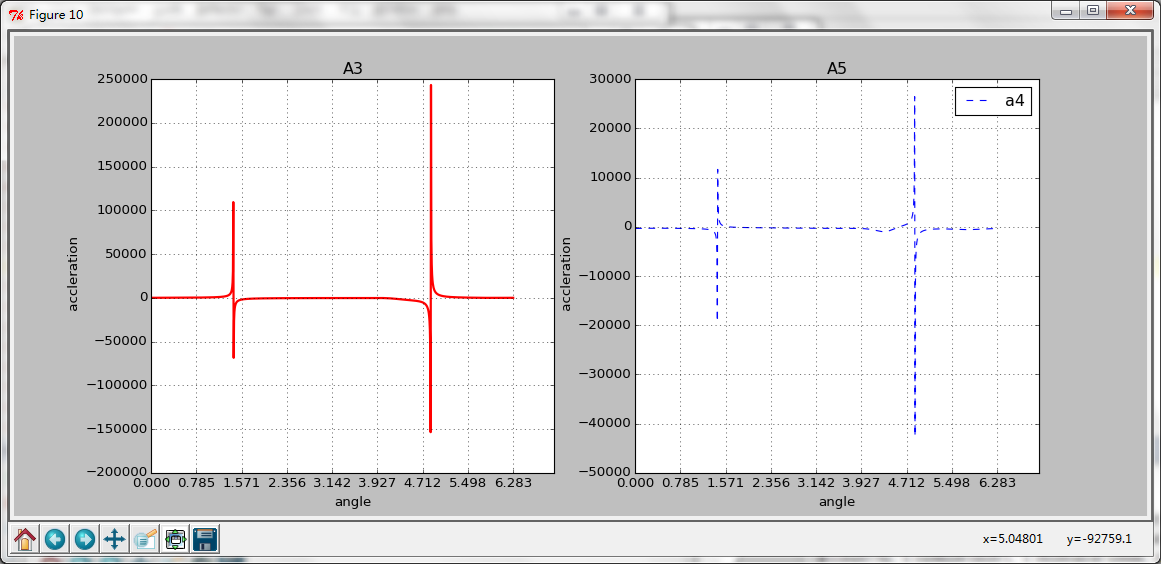
A3的角加速度（好像有个峰值= =、、、）

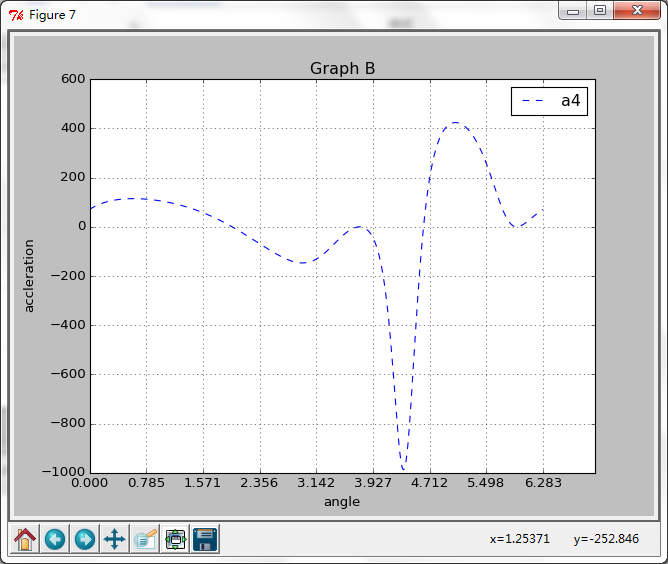
A4的角加速度（小多啦= =、、）

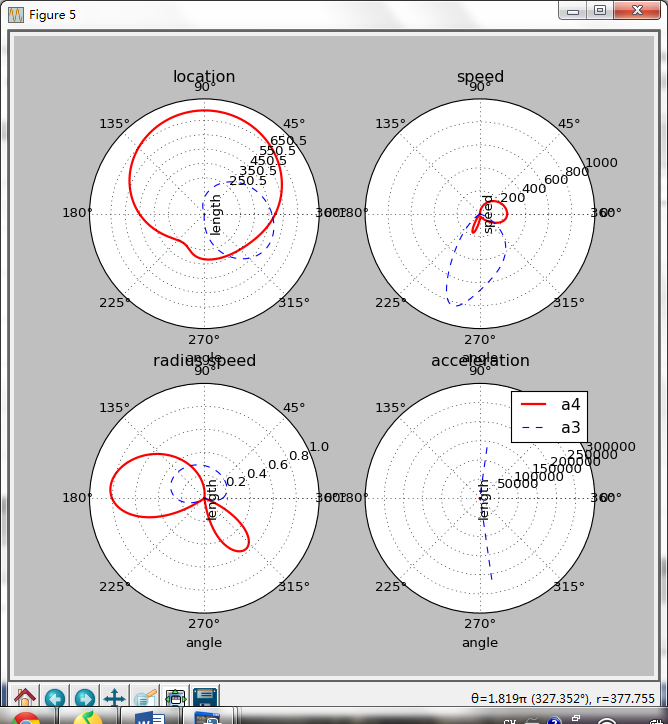
由于这个是周期性的 表示本弱画了一张极坐标图片！

A3和A5的加速度分析

最后附上Python源码（python写的略挫不要介意= =、、、）：

__author__ = 'kido'
import numpy
from numpy import dot
from scipy.optimize import fsolve
from matplotlib.ticker import MultipleLocator
from math import cos
from math import sin
from math import asin
from math import sqrt  # using hudu!
import math
import matplotlib.pylab as plt
import threading
def draw1():
    plt.figure(1)  # location
    plt.plot(lio1, lis3, label="s3", color="red", linewidth=2)
    plt.plot(lio1, lis5, "b--", label="s5")
    plt.xlabel("angle")
    plt.ylabel("length")
    plt.title("length of data")

    plt.legend()
    plt.show()

def draw2():
    plt.figure(2)  # linear speed
    plt.plot(lio1, liv3, label="v3", color="red", linewidth=2)
    plt.plot(lio1, liv5, "b--", label="v5")

    plt.xlabel("angle")
    plt.ylabel("linear speed")
    plt.title("Graph B")

    plt.legend()
    plt.show()

def draw3():
    plt.figure(3)  # radius speed
    plt.plot(lio1, liw3, label="w3", color="red", linewidth=2)
    plt.plot(lio1, liw4, "b--", label="w4")

    plt.xlabel("angle")
    plt.ylabel("Radius speed")
    plt.title("Graph B")

    plt.legend()
    plt.show()

def draw4():
    plt.figure(4)  # radius accerlation
    plt.plot(lio1, lia3, label="a3", color="red", linewidth=2)
    plt.plot(lio1, lia4, "b--", label="a4")

    plt.xlabel("angle")
    plt.ylabel("accleration")
    plt.title("Graph B")

    plt.legend()
    plt.show()

def gauss(a, b):
    n = len(b)
    for i in range(0, n - 1):
        for j in range(i + 1, n):
            # print a[j,i]
            if a[j, i] != 0.0:
                lam = float(a[j, i]) / a[i, i]
                a[j, (i + 1):n] = a[j, (i + 1):n] - lam * a[i, (i + 1):n]
                b[j] = b[j] - lam * b[i]
    for k in range(n - 1, -1, -1):
        b[k] = (b[k] - dot(a[k, (k + 1):n], b[(k + 1):n])) / a[k, k]
    result = b
    return result

def foo(x):
    # s3,s5,o3,o4 =x.tolist()
    s3 = float(x[0])
    s5 = float(x[1])
    o3 = float(x[2])
    o4 = float(x[3])
    return [
        l4 * cos(o4) + s3 * cos(o3) - h2 - l1 * cos(o1),
        l4 * sin(o4) + s3 * sin(o3) - h1 - l1 * sin(o1),
        l4 * cos(o4) + l3 * cos(o3) - s5,
        l4 * sin(o4) + l3 * sin(o3) - h
    ]

# -----main function-----
print 'Now please input your number,indivivually AB,CD,DE,h,h1,h2 :)\nattention : use , under English Input type!'
lis3 =[]
liw3 =[]
liw4 =[]
liv3 =[]
lis5 =[]
liv5 =[]
lia3 =[]
lia4 =[]
lio1 =[]
lia5 =[]
liap3 =[]
il1, il3, il4, ih, ih1, ih2 = input()
l1 = float(il1)
l3 = float(il3)
l4 = float(il4)
h = float(ih)
h1 = float(ih1)
h2 = float(ih2)
o1 = 0
w1 = 1
print '# Make Sure : ', l1, l3, l4, h, h1, h2
print '# Radius rate is : ', w1, 'rad/s'
print '# Guessing matrix : ', [l3 * h1 / h, l4 + sqrt(l3 * l3 - h * h), asin(h / l3), 0]
while (o1     lio1.append(o1)
    result = fsolve(foo, [l3 * h1 / h, l4 + sqrt(l3 * l3 - h * h), asin(h / l3), 0])
    #print '# Bais : ', max(foo(result))
    s3, s5, o3, o4 = result  #get !
    #print "result", result
    #-----------storage data------------
    lis3.append(s3)
    lis5.append(s5)

    #-----------calcualte Rate----------
    x = numpy.matrix([[cos(o3), 0 - s3 * sin(o3), 0 - l4 * sin(o4), 0], [sin(o3), s3 * cos(o3), l4 * cos(o4), 0],
                      [0, 0 - l3 * sin(o3), 0 - l4 * sin(o4), -1], [0, l3 * cos(o3), l4 * cos(o4), 0]],
                     dtype=numpy.float)
    #print x
    aa = numpy.matrix([[cos(o3), 0 - s3 * sin(o3), 0 - l4 * sin(o4), 0], [sin(o3), s3 * cos(o3), l4 * cos(o4), 0],
                       [0, 0 - l3 * sin(o3), 0 - l4 * sin(o4), -1], [0, l3 * cos(o3), l4 * cos(o4), 0]],
                      dtype=numpy.float)
    y = numpy.array([0 - l1 * sin(o1), l1 * cos(o1), 0, 0], dtype=numpy.float)
    #print y
    rad = gauss(x, y)
    ds3 = numpy.float64(rad[0])
    w3 = numpy.float64(rad[1])
    w4 = numpy.float64(rad[2])
    ds5 = numpy.float64(rad[3])
    #----storage the data------
    liw3.append(w3)
    liw4.append(w4)
    liv3.append(ds3)
    liv5.append(ds5)

    #print "at this point " + "w3 :", w3, "w4", w4
    #------calculating accleration-------
    poi = numpy.matrix([[0 - w3 * sin(o3), 0 - ds3 * sin(o3) - s3 * w3 * cos(o3), 0 - l4 * w4 * cos(o4), 0],
                        [0 - w3 * cos(o3), 0 - ds3 * cos(o3) - s3 * w3 * sin(o3), 0 - l4 * w4 * sin(o4), 0],
                        [0, 0 - l3 * w3 * cos(o3), 0 - l4 * w4 * cos(o4), 0],
                        [0, 0 - l3 * w3 * sin(o3), 0 - l4 * w4 * sin(o4), 0]], dtype=numpy.float)
    new = dot(poi, rad)*(-1) + numpy.matrix([0 - l1 * w1 * cos(o1), 0 - l1 * w1 * sin(o1), 0, 0], dtype=numpy.float)
    #print new
    aspe = gauss(aa, new)
    #print "gauss : ", aspe
    #-------------storage data-------
    a3 = float(aspe[0, 1])
    a4 = float(aspe[0, 2])
    lia3.append(a3)
    lia4.append(a4)
    liap3.append(float(aspe[0,0]))
    lia5.append(float(aspe[0,3]))
    #---spin a new round!----
    o1 += math.pi / 500
    #lio1.append(o1)

#--------draw a picture?
print "lis5", lis5
print "lis3", lis3
print "lio1", lio1
plt.figure(6)
plt.subplot(111,polar=True)
plt.plot(lio1, liap3, label="a3", color="red", linewidth=2)
plt.plot(lio1, lia5, "b--", label="a5")
plt.xlabel("angle")
plt.ylabel("length")
plt.title("A5's acceleration")

#plt.thetagrids([0,45])
ax=plt.gca()
ax.xaxis.set_major_locator(MultipleLocator(numpy.pi/4))

plt.figure(5,figsize=(8,8))
plt.subplot(221,polar=True)
plt.plot(lio1, lis3, label="s3", color="red", linewidth=2)
plt.plot(lio1, lis5, "b--", label="s5")
plt.xlabel("angle")
plt.ylabel("length")
plt.title("location")
maxn=numpy.max(lis3)
minn=numpy.min(lis3)
plt.rgrids(numpy.arange(minn,maxn,100),angle=45)
#plt.thetagrids([0,45])
ax=plt.gca()
ax.xaxis.set_major_locator(MultipleLocator(numpy.pi/4))

plt.subplot(222,polar=True)
plt.plot(lio1, liv3, label="v3", color="red", linewidth=2)
plt.plot(lio1, liv5, "b--", label="v5")
plt.xlabel("angle")
plt.ylabel("speed")
plt.title("speed")
maxn=numpy.max(liv3)
minn=0-numpy.min(liv3)
#plt.rgrids(numpy.arange(minn,maxn,100),angle=45)
#plt.thetagrids([0,45])
ax=plt.gca()
ax.xaxis.set_major_locator(MultipleLocator(numpy.pi/4))

plt.subplot(223,polar=True)
plt.plot(lio1, liw4, label="w4", color="red", linewidth=2)
plt.plot(lio1, liw3, "b--", label="w3")
plt.xlabel("angle")
plt.ylabel("length")
plt.title("radius speed")
maxn=numpy.max(liw3)
minn=numpy.min(liw3)
#plt.rgrids(numpy.arange(minn,maxn,100),angle=45)
#plt.thetagrids([0,45])
ax=plt.gca()
ax.xaxis.set_major_locator(MultipleLocator(numpy.pi/4))

plt.subplot(224,polar=True)
plt.plot(lio1, lia4, label="a4", color="red", linewidth=2)
plt.plot(lio1, lia3, "b--", label="a3")
plt.xlabel("angle")
plt.ylabel("length")
plt.title("acceleration")

#plt.rgrids(numpy.arange(minn,maxn,100),angle=45)
#plt.thetagrids([0,45])
ax=plt.gca()
ax.xaxis.set_major_locator(MultipleLocator(numpy.pi/4))
plt.legend()

plt.figure(1)  # location
plt.plot(lio1, lis3, label="s3", color="red", linewidth=2)
plt.plot(lio1, lis5, "b--", label="s5")
plt.xlabel("angle")
plt.ylabel("length")
plt.title("length of data")
plt.grid()
ax=plt.gca()
ax.xaxis.set_major_locator(MultipleLocator(numpy.pi/4))

plt.legend()
#plt.show()

plt.figure(2)  # linear speed
plt.plot(lio1, liv3, label="v3", color="red", linewidth=2)
plt.plot(lio1, liv5, "b--", label="v5")

plt.xlabel("angle")
plt.ylabel("linear speed")
plt.title("Graph B")
plt.grid()

ax=plt.gca()
ax.xaxis.set_major_locator(MultipleLocator(numpy.pi/4))

plt.legend()
#plt.show()

plt.figure(3)  # radius speed
plt.plot(lio1, liw3, label="w3", color="red", linewidth=2)
plt.plot(lio1, liw4, "b--", label="w4")

plt.xlabel("angle")
plt.ylabel("Radius speed")
plt.title("Graph B")
plt.grid()
ax=plt.gca()
ax.xaxis.set_major_locator(MultipleLocator(numpy.pi/4))
plt.legend()
#plt.show()

plt.figure(4)  # radius accerlation
plt.plot(lio1, lia3, label="a3", color="red", linewidth=2)
print "lio1 :",lio1
print "lia3 :",lia3
print "lia4 :",lia4
plt.xlabel("angle")
plt.ylabel("accleration")
plt.title("Graph B")
plt.grid()
ax=plt.gca()
ax.xaxis.set_major_locator(MultipleLocator(numpy.pi/4))
plt.legend()

plt.figure(7)  # radius accerlation

plt.plot(lio1, lia4, "b--", label="a4")

plt.xlabel("angle")
plt.ylabel("accleration")
plt.title("Graph B")
plt.grid()
ax=plt.gca()
ax.xaxis.set_major_locator(MultipleLocator(numpy.pi/4))
plt.legend()

plt.figure(10)  # radius accerlation
plt.subplot(121)
plt.plot(lio1, lia5, label="a3", color="red", linewidth=2)
plt.xlabel("angle")
plt.ylabel(" accleration")
plt.title("A3")
plt.grid()
ax=plt.gca()
ax.xaxis.set_major_locator(MultipleLocator(numpy.pi/4))
plt.subplot(122)
plt.plot(lio1, liap3, "b--", label="a4")
plt.xlabel("angle")
plt.ylabel(" accleration")
plt.title("A5")

plt.grid()
ax=plt.gca()
ax.xaxis.set_major_locator(MultipleLocator(numpy.pi/4))
plt.legend()

plt.show()