前言
很久都没有用过numpy来做科学计算了,现在Python的机器学习这么火,而机器学习很多代码都需要用numpy、scipy来构建,所以我现在开始进行一些温习吧
ndarray对象
创建
我们需要创建数组并且对其进行操作。
我们可以通过给array函数传递python的序列对象创建数组,如果传递的是多层嵌套序列,将创建多维数组。
数组的类型可以通过dtype来获取:
数组的大小可以通过shape获得或者修改:
这里的大小和列表的大小保持一致。而当变更shape的时候,例如(3,4)->(4,3)的时候,并不是对数组进行转置,而只是改变每个轴的大小,数组元素在内存中的位置并不发生改变。
当某个轴为-1的时候,蒋根据数组元素的个数自动计算此轴的长度,也就是说,如果你变更的shape是2,-1那么其就会自动计算为2,6
使用数组的reshape的方法,可以创建一个变更尺寸的新数组,而原数组的shape保持不变。但是新数组和原数组仍然共享数据存储内存区域,所以修改任意一个数组的元素都会变更另一个数组的内容。
数组的元素可以通过dtype属性获得,上面例子中的参数序列的元素都是int,因此创建的数组的元素类型也是整数,你可以通过指定dtype参数来指定元素类型。
numpy中的数据类型转换,不能直接改原数据的dtype。只能用函数astype()。
而python会自带一些函数来创建数组,可以不需要使用python对象转换为array对象。
arange
类似于range,通过指定开始、结果以及步长来创建一个一维数组。
linspace
通过开始设置开始、终值和元素个数来创建等差一维数组,可以通过设置endpoint来指定是否包括终值。
logspace
和linspace一样,不过创建等比数列。下面这个例子产生1(10^0)到100(10^2),有20个元素的等比数列。
其他
此外使用frombuffer,fromstring,fromfile等函数可以从字节中创建数组
下面以fromstring为例子,在Python之中,字符串实质上是字节序列,每个字符占一个字节,如果从字符串中创建一个64bit的整数数组的话,所得到的数组正好是字符串中每个ASCII编码:
如果从字符串中创建一个16bit的整数数组,那么相邻的两个字节就表示一个证书,把字节98和97当做一个16bit的证书,那么他的值就是98256+97=25185。可以看出内存中是以*低位字节在前(little endian)的方式保存数据的。
当然,我们使用C语言的二进制写了一组double类型的数值的时候,我们读文件的时候,需要通过fromstring函数将其转换为float64类型的数组。
函数创建数组
fromfunction函数的第一个参数为每个数组元素的函数,第二个参数为数组的大小(其支持多维数组),所以第二个数组必须为一个元祖。
一维:
二维:
存取元素
数组元素的存取方式和Python标准的标准相同:
使用整数下标获取数组中某个元素
|
|
获取数组的一个切片,左半闭集
|
|
省略开始下标,表示从a[0]开始
表示数组从后向前数
范围中的第三个参数为步长,隔一个参数取一个元素,步长为负的时候,开始下表必须大于结束下标
和Python序列不同,通过下标范围获取的新数组仍然和原始数组共享一块数据空间,修改的方式和上面一致。
使用整数序列
当使用整数序列对数组元素进行存储的时候,将使用整数序列的每个元素作为下标,整数序列可以是列表或者数组,新数组和原始数组不共享数据空间。
在上面的第三个例子之中,获取x中下标为3,3,1,8的4个元素,组成一个新的数组。
bool数组
当使用bool数组作为下标取数组x中的元素时,将收集数组x中所有在数组b中对应下标为True的元素,使用bool数组作为下标获得的数组不和原始数组共享数据空间。
这里是bool数组,bool数组的下标为0,2的元素为True,因此获取a中下标为0,2的元素
上面是bool列表,把True当做1,False当做0,按照整数序列方式获取a中的元素。
同样的bool数组也可以用来修改元素。
这里说明的是,bool数组一般不是手工产生,而是使用bool运算的ufunc函数产生。
x>0.5会将数组中的每个元素和0.5进行比较,得到一个bool数组,True表示x中对应的值大于0.5。
而x>0.5返回的bool数组收集x中的元素,其返回所有大于0.5的元素的数组。
多维数组
多维数组存取和一维数组类似,因为其具有多个轴,因此它的下标需要多个值来表示,Numpy采用元祖(tuple)作为数组的下标。
需要指出的是元祖是不需要圆括号的。例如x,y=y,x就是用元祖来交换变量值的一个例子。
使用数组切片语法访问多维数组的元素。那么可以使用下面的语句来创建这个数组。
这个语句就会创建下面这样的数组:
首先上面的加数创建了一个竖列的数组,而加上了一个横列的数组就变成了这样了。
取多维数组的方式和取一维原理类似,都是可以通过索引值取某一列或行切片取某一列或一行,你可以想象成一个横竖线所交汇或者围成矩形的位置就是所取的数组。
a[(0,1,2,3,4)(1,2,3,4,5)]:用于存取数组下标和仍然是一个有两个元素的元祖,元祖中的每个元素都是整数序列,分别对应于数组的第0轴和第1轴.从两个序列的对应位置取出两个证书组成下标:a[0,1],a[1,2]...
a[3:,[0,2,5]]:下标中的第0轴是一个范围,其选取第三行之后的所有行,他选取第0,2,5三列。
在进行存取的时候也是可以使用Bool数组来存储的。
结构数组
在C语言之中可以通过struct关键字定义结构类型,结构中的字段占据连续的内存空间,每个结构体占用的内存大小都相同,因此可以很容易的定义结构数组。只要numpy中的结构定义和C语言中的定义相同,Numpy就可以很方便的读取C语言的结构数组的二进制数据,转换为numpy的结构数组。
在创建对象personType,其通过字典参数描述结构类型的各个字段,字典中有两个关键字,names,formats,每个关键字对应的值都是一个列表。names定义结构中的每个字段名,formats则是定义每个字段的类型。这里我们援引numpy的官方指南,给出formats的字符串所代表的意思:
- ‘b’boolean 布尔值
- ‘i’(signed) integer 有符号的整数
- ‘u’unsigned integer 无符号的整数
- ‘f’floating-point 浮点数
- ‘c’complex-floating point 复数浮点数
- ‘O’(Python) objects Python对象
- ‘S’, ‘a’(byte-)string X字节的字符串
- ‘U’Unicode unicode对象
- ‘V’raw data (void) 空
然后我们调用array创建数组,通过关键字参数dtype指定所处案件数组的元素类型。而在struct之中,我们常常用以下符号来描述字段值的字节顺序:
- | 忽视字节顺序
- < 低位字节在前
高位字节在前
结构数组的存取方式和一般数组相同,通过索引或者字段可以取得元素,此时元素是一个结构,这里可以像字典一样通过字符串下标取得或者修改对应的字段值。
我们不但可以获得结构元素的某个字段,还可以直接获得结构数组的字段,其返回的是原始数组的师徒,因此可以通过修改a[0]改变a[0][“age”]。
通过调用a.tostring或者a.tofile的方法,可以直接输出数组a的二进制形式,并且可以利用下面的C代码提取处文件数据。
内存对齐
C语言结构为了寻址方便,会自动的添加一些用于填充的字节,这个被称为内存对齐。由于内存对齐问题,在name和age中间会填充两个字节,最终的结构体大小不变。因此为了解决numpy所配置的内存大小不符合C语言对齐规范,可以在创建dtype对象的时候,传递参数align = True,这样内存对齐问题就能够解决了。
结构类型之中也可以包括其他的结构类型,下面的语句创建一个有一个字段的f1的结构,f1的值是另一个结构,他有字段f2,其类型为16bit整数。
ufunc运算
ufunc是universal function的缩写,其能够对数组每个元素进行操作的函数,numpy内置的许多ufunc函数都是在C语言的层面上实现的,所以他们的计算速度非常的快。
先用linspace产生一个从0到$$2\pi$$的等距离的10个数,然后将其传递给sin函数,由于其是一个ufunc函数,因此他对x的每个元素求正弦值并且返回结果,赋值给y,计算后x值没有改变,而是新创建了一个数组,如果我们希望覆盖的话,可以把被覆盖的数组作为第二个参数传递给ufunc函数。
那么我们来比较一下numpy.sin和Python标准库math.sin的计算速度:
最终的结果numpy比标准的math库快太多了。
这得利于numpy.sin在C语言级别的循环运算,numpy.sin同样也支持单个数值求正弦,但是比math.sin慢多了:
代码如下
结果:
注意的是numpy.sin的计算速度只有math.sin的1/10,这是因为numpy.sin支持数组和单个计算,其C语言内部实现比math.sin复杂很多,如果我们在同样的Python级别进行循环的话,就会看出差异了。
另外,numpy.sin返回的类型是numpy.float64而math.sin则是返回标准的float型。
numpy之中还有各式各样的函数来提供计算,除了sin这种单输入函数外,还有其他的,诸如add这种函数,add会把两个等shape的array每个元素对应想家,和sin一样,如果你要覆盖的话,指定第三个参数为覆盖的数列就可以了。
| + | 加法 |
| - | 减法 |
| 乘法 | |
| / | 根据是否激活future_.division分为整数的除法和浮点数的除法 |
| // | 总是对除法的商求整 |
| * | 幂函数 |
| % | 取余 |
根据Python的重载规则,add可以简写为a+b。
通过对于ufunc的调用,可以实现各种算式的数值计算,而有时候这种算式不容易编写,而针对Python的计算函数却很容易使用Python实现,这个时候就可以用fromfunc函数将一个计算单元的函数转换成ufunc函数来对数组进行计算了。
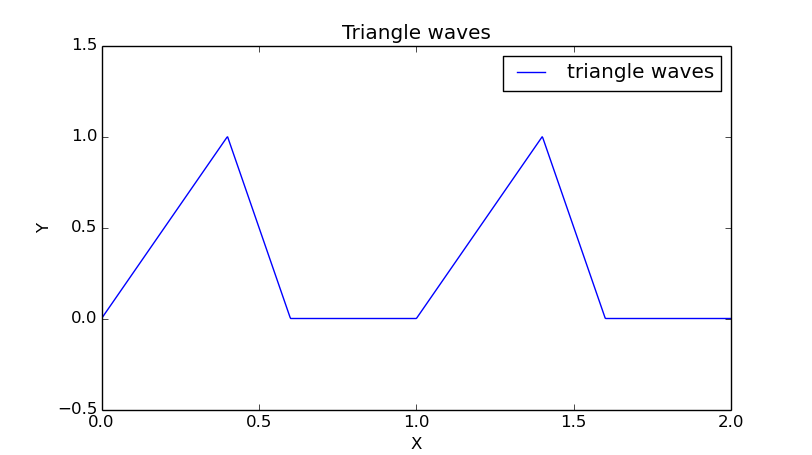
下面我们演示一个分段函数,也就是三角波。
我们很容易就给出了三角波的函数:
显然triangleWave只能计算单个数值,而无法对数组进行处理,我们可以使用下面的方法先使用列表包容,计算出一个list,然后使用array函数把列表转换为数组:
这种做法每次都需要使用列表包容来调用函数,对于多维数组而言是非常麻烦的,我们就可以使用frompyfunc来解决这个问题。
frompyfunc的调用格式为frompyfunc(func,nin,nout),其中func是计算单个元素的函数,nin是输入参数的个数,nout是输出的个数,这里由于c,c0,hc都是固定值,所以我们用一个lambda函数进行包装。不过还有一种方法:
我们通过函数triangleFunc包装三角波的三个参数,在其内部定义一个三角波函数trifunc。trifunc函数会在调用的时候采用triangleFunc的参数进行计算,最后其返回一个frompyfunc的转换结果。
需要主意的是用frompyfunc的得到的函数计算出的数组元素为object,所以还需要再次y2.astype(numpy.float64) 将其转换为双精度浮点数。
广播
当我们使用ufunc函数队两个数组进行计算的时候,ufunc会对这两个数组对应的元素进行计算,因此它要求这两个数组具有相同的大小,若两个数组的大小不同的话,会进行下面的广播处理:
- 让所有的输入数组都想其中shape最长的看齐,shape中不足的部分通过加1补齐
- 输出数组的shape是输入数组shape各轴上的最大值
- 如果输入数组的某个轴和输出数组对应轴的长度相同或者其长度为1时,这个数组能够用来计算,否则出错
- 当输入数组的某个轴长度为1时,沿着此轴运算时都能够用此轴上的第一组值
那么还是给出栗子把:
先创建一个二维的数组a,其shape为6,1,创建一个一维数组b,其shape为5, ,计算a和b的和,得到一个加法表,其相当于计算a,b中所有元素的和,得到一个shape为6,5的数组:
由于a,b的shape长度(也就是ndim属性)不同,根据规则1,需要让b的shape向a对齐,于是将b的shape前面加1,补齐为(1,5).相当于做了以下计算:
这样加法运算的两个输入数组的shape分别为(6,1)和(1,5),根据规则2,输出数组的各个轴的长度为输入数组各个轴上的长度的最大值,可知输出数组shape为(6,5)。
由于b的第0轴上的长度为1,而a的第0轴的长度为6,因此为了让它们在第0轴上能够相加,所以需要将b在第0轴的长度扩展为6,这相当于:
由于a的第1轴的长度为1,而b的第1轴长度为5,因此为了让它们在第1轴上能够相加,需要将a在第1轴上的长度扩展为5,这相当于:
经过上述处理之后,a和b就可以按照对应元素进行相加运算了。
当然,在numpy内部不会真正的将长度为1的轴用repeat函数进行扩展,如果这样做的话就太浪费空间了。
由于这种广播计算很常用,因此numpy提供了一个快速产生如上面a,b数组的方法:ogrid对象。
ogrid是一个非常有趣的对象,它像一个多维数组一样,用切片组元作为下标作为下标进行存取,返回的是一组可以用来广播计算的数组。其切片下标有两种形式:
- 开始值:结束值:步长(和
numpy.arange类似) - 开始值:结束值:长度j,当第三个参数为虚数的时候,其会返回的数组的长度(和
numpy.linspace类似)
orgid为什么不是函数
利用ogrid的返回值,我能很容易计算x,y网格面上各点的值,或者x,y,z网格体上各点的值。上面是回执三维曲面$$xe^{x^{2}-y^{2}}$$的程序:
ufunc的方法
ufunc还有其他的用法,这种方法只对两个输入一个输出的ufunc函数有效,其他的ufunc对象调用这些方法会抛出ValueError异常。
reduce方法和Python的reduce函数类似,他会沿着axis轴对array进行操作,相当于将
例如:
还有针对多维的reduce:
accumulate方法和reduce方法类似,只是它返回的数组和输入的数组的shape相同,保存所有的中间计算数组。
reduceat方法计算多组reduce的结果,通过indices参数指定一系列reduce的起始和终了位置:
对于indices中的每个元素会调用reduce计算出一个值来,因此最终的计算结果的长度和indices的长度相同。出了最后一个元素以外,都按照下列计算得出:
而对于最后一个元素如下计算:
因此下面的例子中,结果的每个元素如下计算而得
可以看出result[::2] 和a相等,而result[1::2] 和numpy.add.accumulate(a)相等。
outer方法,<op>.outer(a,b)方法的计算等同于如下程序:
其中squeeze的功能是剔除数组a中长度为1的轴。
可以看出通过outer的方法计算的结果是乘法表。乘法表最终是通过广播的方法计算出来的。
矩阵运算
NumPy和Matlab不一样,对于多维数组的运算,缺省状况下并不使用矩阵运算,如果你希望对数组进行矩阵运算的话,可以调用相应的函数。
matrix对象
numpy提供了
matrix类,使用matrix类创建的是矩阵对象,它们的加法乘除运算缺省用的是矩阵方式计算,因此用法和matlab十分类似。由于NumPy中同事存在ndarray和matrix对象,因此用户很容易将两者弄混。这和Python的“显式优于隐式”的原则,因此并不推荐在较为复杂的程序之中使用matrix。
矩阵的乘法可以使用dot函数进行计算,对于二维数组,他计算的是矩阵乘积,而一维则是点积。当需要将一维数组当做列向量或者行向量进行矩阵计算的时候,推荐先使用reshape函数将一维数组转换为二维数组。
除了dot计算乘积以外,NumPy还提供了inner和outer等多种计算乘积的函数。这些函数计算乘积的方式不同,尤其是当对于多维数组的时候更容易弄混。
dot
对于两个一维数组,计算的是这两个数组对应的下标元素的乘积和(内积),对于二维数组,计算的是两个数组的矩阵乘;对于多维数组,他的通用计算公式如下,即结果数组中的每个元素都是:数组a的最后一维上的所有元素与数组b的倒数第二位上的所有元素的乘积和:
下面以两个三维数组乘积演示一下dot乘积的计算结果:
首先创建两个三维数组,这两个数组的最后两维满足矩阵乘积的条件:
dot乘积的结果c可以视为分组矩阵的乘积:
inner
和dot乘积一样,对于两个一维数组,计算的是这两个数组对应下标元素的乘积和;对于多维数组,它计算的结果数组中的每个元素都是:数组a和b的最后一维的内积,因此数组a和b的最后一维的长度必须相同:
下面的是inner乘积的演示:
矩阵中更高及的一些运算可以在Numpy线性代数字库linalg中找到。例如inv函数计算矩阵逆,slove函数可以用于求解多元一次方程组:
solve函数有两个参数a,b。a是一个$$N*N$$的二维数组,而b是一个长度为$$N$$的二维数组,solve函数找到一个长度为N的一维数组x,使得a和x的矩阵乘积正好等于b,数组x就是多元一次方程组的解。