前言
SVM,支持向量自动机,是目前分类器不加修改可以直接使用的最好的现成的分类器。其中最流行的一种实现,也就是序列最小优化(Sequential Minimal Optimization)算法。
基于最大间隔分隔数据
特点
优点
泛化错误率低,计算开销不打,结果易解释。
缺点
对参数调节和核函数的选择比较敏感,原始分类器不加修改的话只能用于处理二类问题
适用类型
数值型和标称型数据
线性可分
我们首先需要解释线性可分的这个概念,先考虑A中两组数据,它们之间已经分隔的足够开,因此很容易可以在途中画出一条曲线将这两组数据点分开。这种情况下,这组数据被成为线性可分(linearly separable)数据。
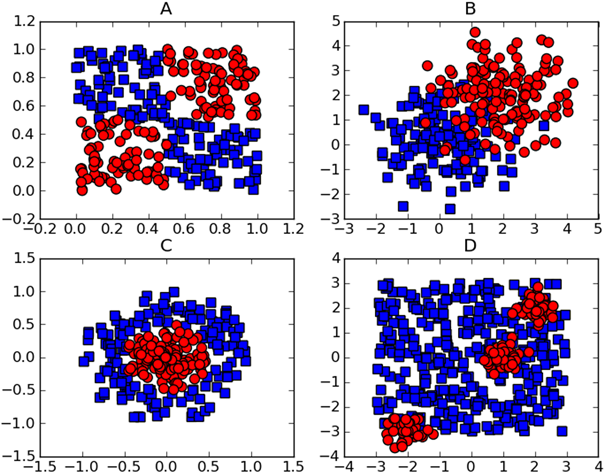
上述将数据集分隔开来的直线成为分隔超平面(separating hyperplane)。在上面给出的例子中,由于数据点都在二维平面上,所以此时分隔超平面就只是一条直线。但是,如果所给的数据是三维的,那么就是一个平面。这个时候分隔超平面也就是作为分类的决策边界,分布在超平面一侧的所有数据都属于某个类别,而分布在另一侧的所有数据则属于另一个类别。
下面给出了线性可分的数据集的几种划分方式。
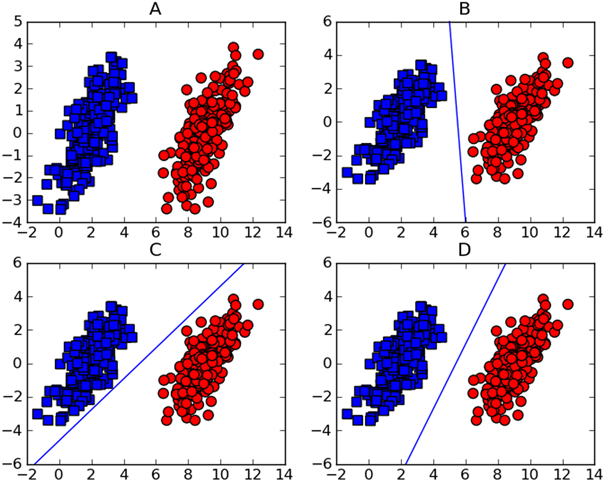
这个时候,如果数据点离决策边界越远,那么其最后的预测结果也就越可信。但是考虑到B到D中的三条直线,他们都能够将数据分隔开,但是哪个会更好呢?是不是有点寻找最佳拟合直线的感觉,是的,上述做法确实有点像直线拟合,但这并不是最佳的方案。这个时候我们希望找到离分隔超平面最近的点,确保他们离分隔面的距离尽可能的远。同时我们也希望间隔尽可能的大,这样我们的分类器也能足够的健壮。
支持向量就是离分隔超平面最近的那些点。接下来试着就需要最大化支持向量到分隔面的距离。
寻找最大间隔
分隔超平面的形式可以写成( w^{T}x+b )。如果要计算点A到分隔超平面的距离,就必须给出点到分隔面的法线或者垂线的长度。这个值应该是( |w^{T}A+b|/||w|| )。这里的常熟b类似于logistic回归中的截距。这里向量w和b一起描述了所给数据的分割线或者超平面。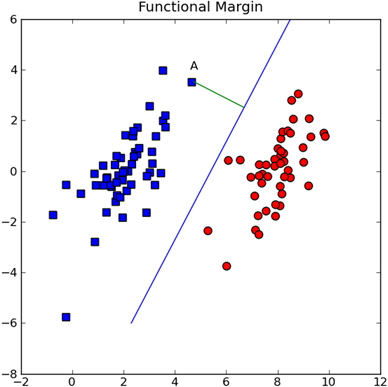
分类器求解的优化问题
输入数据给分类器会输出一个类别标签,这相当于一个Sigmoid的函数在作用。下面将使用类似单位阶跃函数的函数对( w^{T}x+b )作用得到( f(w^{T}x+b) ),其中当u<0时候f(u)输出-1,反之则输出+1。这和前一章的Logistic回归有所不同,那里的类别标签是0和1。
这里的类别标签为什么采用-1和+1而不采用0和1呢?这是由于-1和+1仅仅相差一个符号方便数学上的处理,这个时候可以通过一个统一的公式来表示间隔或者数据点到分隔超平面的距离,同时不需要担心数据到底是属于+1还是-1.
当计算数据点到分隔面的距离并且确定分隔面的放置位置时候,间隔通过( label\times (w^{T}x+b) )来计算,这个时候就能体现出-1和+1类的好处了。如果数据点处于正方向并且离分隔超平面很远的位置时候,( w^{T}x+b )将会是一个很大的正数,同时( label\times (w^{x}+b) )也会是一个很大的正数。如果处于负方向并且离超平面很远的位置的时候,类别标签是-1,则( label\times (w^{T}x+b))仍然是一个很大的正数。
现在的目标就是找出分类器定义的w和b。为此,我们必须找到具有最小间隔的数据点,这些数据点也就是前面提到的支持向量。一旦找到具有最小间隔的数据点,我们就需要对这个间隔最大化,这样可以写作:[ \arg \max\limits{w,k}\left\lbrace \min\limits{n}(label\cdot (w^{T}x+b))\cdot \frac{1}{\left| \left| w\right| \right| } \right\rbrace]直接求解上述问题相当困难,所以我们将其转换成一个更容易求解的方法。首先考虑一下式子中大括号的部分。由于对乘积进行优化是一种很复杂的事情,因此我们要做的事情就是固定其中的一个因子来最大化另一个因子。如果令所有支持向量的( label \times (w{T}x+b))都等于1,那么就可以通过(||w||{-1})的最大值来的到最终解。但是并非所有的数据点( label \times (w{T}x+b))都等于1,只有那些离分隔超平面最近的点得到的值才是1。离超平面越远的数据点,其( label \times (w{T}x+b))的值也越大。
再上面的优化问题中,给定了一些约束条件然后求最优值,因此该问题是一个带约束条件的优化问题。这里的约束条件就是( label*(w^{T}x+b)\geq 1.0 )。对于此类优化问题,有一个非常著名的求解方法,就是拉格朗日乘子法。通过引入拉格朗日乘子,我们就可以基于约束条件来表述原来的问题。由于这里的约束条件都是基于数据点的,因此我们就可以把超平面写成数据点的形式。于是优化目标函数可以写成:[\max\limits{\alpha}\left[ \sum{i=1}^{m}\alpha -\frac{1}{2}\sum{i,j=1}^{m}label^{(i)}\cdot label^{(j)}\cdot a{i}\cdot a{j}\left\langle x^{(i)},x^{(j)} \right\rangle\right]]其约束条件为:[\alpha \geq 0,\sum{i-1}^{m}\alpha_{i}\cdot label^{(i)}=0]
至此,这个非常完美,但是这里有个假设就是:数据必须是100%线性可分。目前未知,我们都知道所有的数据都不那么干净,所以我们可以通过引入所谓的松弛变量(slack variable),来允许有些数据点可以处于分隔面的错误的一侧。这样我们的优化目标就能过保持不变,但是此时的约束条件则变为:[C\geq\alpha \geq 0,\sum{i-1}^{m}\alpha{i}\cdot label^{(i)}=0]这里的常数C用于控制最大化间隔和保证大部分的函数间隔小于1.0这两个目标的权重。在优化算法的实现算法的实现代码中,常数C是一个参数,因此我们就可以通过调节这个参数得到不同的结果,一但求出了所有的alpha,那么分隔超平面就可以通过这些alpha表达。这个问题十分直接,SVM中的主要工作就是求出这些alpha。
SVM应用的一般框架
我们需要给出SVM的一般流程:
- 收集数据:任何方法
- 准备数据:需要数值型数据
- 分析数据:有助于可视化分隔超平面
- 训练算法:SVM大部分时间都源于训练,这个过程主要实现两个参数的调优
- 测试算法:十分简单的计算过程就能够实现
- 使用算法:几乎所有分类问题都可以使用SVM,值得一提的是,SVM本身就是一个二类分类器,对多类问题则需要修改代码。
SMO的高效优化算法
我们所需要做的围绕优化的事情就是训练分类器,一旦得到了alpha的最优值,我们就能够得到了分隔超平面(二维平面就是直线)并能用于数据分类。
Platt的SMO算法
SMO,序列最小化。Platt的SMO算法是将大优化问题分解为小优化问题来求解的。这些小问题是比较容易求解的,并且对顺序求解的结果于将他们作为整体求解的结果是完全一致的。在结果完全相同的时候,SMO的算法的求解时间会短很多。
应用简化版算法处理小规模数据集
简化版代码虽然量少但是执行速度慢。Platt SMO算法中的外循环需要确定最佳alpha对。而简化版则会跳过这个部分,首先直接在数据集上遍历每个alpha,然后在剩下的alpha集合中随机选择另一个alpha,从而构建alpha对。这里,我们需要同时改变两个alpha。之所以这样做是因为我们有个约束条件[\sum \alpha_{i}\cdot label^{(i)}=0]由于改变一个alpha可能会导致约束条件失效,所以我们总是同时改变两个alpha。
为此我们将构建一个辅助函数,用于在某个区间范围内随机选择一个整数。同时也需要另一个辅助函数,用于在数值很大时候对其进行调整。下面的程序清单给出了这两个函数的实现。
在testSet.txt文件中保存了之前图片中的数据。接下来我们就将在这个文见上应用SMO算法。第一个函数就是之前熟悉的loadDatSet(),这个函数打开文件并且逐行解析,从而得到每行的类标签和整个数据矩阵。
下一个函数selectJrand()有两个参数值,其中i是第一个alpha的下标,m是所有alpha的数目。只要函数值不等于输入值i,函数就会随机选择。
最后一个辅助函数就是clipAlpha(),它是用于调整大于H或者小于L的alpha值。尽管上述3个辅助函数本身做的事情不多,但是用于分类器却很有用处。
在输入并保存程序清单6-1中的代码之后,运行如下命令:
可以看的出来,这里采用的类别标签是-1和1,而不是0和1
上述工作完成后,就可以使用SMO算法的第一个版本了:
上面是SMO的一个有效版本。在Python中,因为我们代码很长,所以使用了\结尾来表示一行代码。
这个函数非常大。其具有5个输入参数,分别是数据集、类别标签、常数C、容错率和退出前的最大循环次数。
在每次循环中,将alphaPairsChanged设为0,然后再对整个集合顺序遍历。变量alphaPairsChanged用于记录alpha是否进行优化。当然,在循环结束的时候就可以得知这一点。首先,fXi能够计算出来,这就是我们预测的类别。然后,基于这个实例的预测结果和真实结果的比对,就可以计算出误差Ei。如果误差很大,那么可以对该数据实例所对应的alpha值进行优化。在if语句中,不论是正间隔还是负间隔都会被测试。并且在该if语句中,也要同事检查alpha值,以保证其不等于0或者C。由于后面alpha小于0或者大于C会被调整成0或者C,所以一旦在if语句之中他们等于这两个值的话,他们已经就在边界上了,是不值得对其进行优化的。
接下来,可以利用辅助函数来随机选择另一个alpha值,也就是alpha[j]。同样的,可以采用第一个alpha值(alpha[i])的误差计算方法,来计算这个alpha值的误差。这个过程可以通过copy()的方法来实现,因此稍后可以将新的alpha值和老的alpha值进行比较,Python会通过引用的方式来传递所有的列表,所以必须明确的告知Python要为alphaIold和alphaJold分配新的内存,否则的话,再对新值和旧值进行比较的时候,就看不到新旧值的变化。之后我们开始计算L和H,他们用于将alpha[j]调整在0和C之间,如果L=H,就不做任何改变,直接执行continue语句。这在Python中,则意味着本次循环结束直接运行下一次的for循环。
Eta是alpha[j]的最优修改值。如果其为0,那就是说需要退出for循环的当前迭代过程。这个过程对真实的算法进行了简化处理。如果eta为0,那么计算新的alpha[j]就比较麻烦了。然而现实中这种情况却很少发生,因此我们这里忽略这个情况。于是可以计算出一个新的alpha[j]。
然后,就是需要检查alpha[j]是否有轻微的改变。如果是的话,就需要退出for循环,然后同时改变alpha[i]和alpha[j],虽然改变的大小一样,但是方向却正好相反。经过优化之后,就可以队这两个alpha值设定一个常数值。
最后,在优化过程结束的同时,必须确保在合适的时机结束循环。如果程序执行到for循环的最后一行都不执行continue语句,那么就已经成功的改变了一对alpha,同时可以增加alphaPairsChanged的值。在for循环以外,需要检查alpha值是否已经做了更新,如果有更新则设定iter为0后继续运行程序。只有在所有数据集上遍历maxIter次,且不在发生任何alpha修改后,程序才会停止并且退出while循环。
所以可以执行命令
然后会输出:
一旦运行结束,我们可以观察:
我们可以直接观察alpha矩阵本身,但是由于其是一个稀疏矩阵。我们可以观察其大于0的元素以及数量:
由于SMO的随机性,我们得到的数据可能不一样。在原是数据及上对这些支持向量标记之后是这样的:
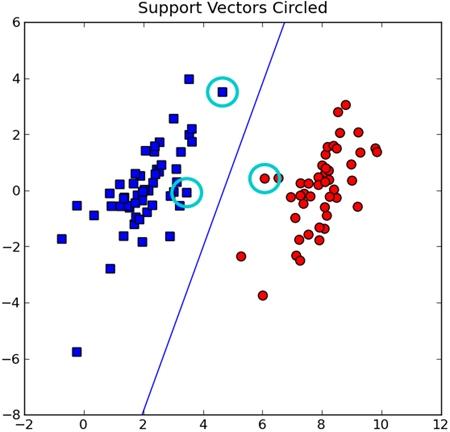
而经过实测发现时间还是略长的。所以我们还是需要完整的SMO算法来加快其运算速度。
利用完整的Platt SMO算法加速优化
在小规模的数据范围内运行简化版的SMO自然是没什么问题的,但是一旦数据集过大就容易GG。现在我们就开始讨论完整版的Platt SMO算法。在这两个版本中,实现alpha的更改和代数运算的优化算法一模一样。在优化过程中,唯一的不同就是选择alpha的方法。完整版的Platt SMO算法应用了一些能够提速的启发方法。
Platt SMO算法是通过一个外循环来选择第一个alpha值的,并且其选择过程会在两种方式之间进行交替:一种方式是在所有数据集上进行单遍扫描,另一种方式则是在非边界alpha中实现单遍扫描。而所谓费边界alpha指的是那些不等于边界0或者C的alpha值。对整个数据集的扫描相当容易,而实现非边界alpha值的扫描的时候,首先需要建立这些alpha值的列表,然后再对这些表进行遍历。同事,这个步骤可以跳过那些已知的不会改变的alpha值。
在选择第一个值alpha后,算法会通过一个内循环来选择第二个alpha值。在优化过程中,会通过最大化步长的方式来获得第二个alpha值。在简化版SMO算法中,我们会在选择j之后计算错误率Ej。但在这里,我们会建立一个全局的缓存用于保存误差值,并从中选择使得步长或者Ei-Ej最大的alpha值。
所以我们应该包含用于清理代码的数据结构和3个用于对E缓存的辅助函数。
首要的事情就是建立一个数据结构来保存所有的重要值,而这个过程可以通过一个对象来完成。这里使用对象的目的是为了作为一个数据结构来使用对象。这样数据就可以通过一个对象来进行传递。实际上,当完成其实现时,可以容易通过Python的字典来完成。但是在访问对象成员变量时,这样做会有更多的手工输入操作,所以我们还是使用一个包含__init__的方法的optStruct类。该方法可以实现成员变量的填充。除了增加一个(m\times 2)的矩阵或者eCache外,这些做法和简化版的SMO一模一样。eCache的第一列给出的是eCache是否有效的标志位,而第二列给出的是实际的E值。
对于给定的alpha值,第一个辅助函数calcEK()能够计算E值并且返回。以前,这个过程是采用内嵌的方法来完成的,但是由于这个过程在这个版本的SMO算法中出现频繁,所以还是写成函数比较好。
下一个函数selectJ()用于选择第二个alpha或者内循环中的alpha值。回想一下,这里的目标实际上是选择第二个alpha值以保证每次优化中采用最大步长。这个函数的误差值与第一个alpha值Ei和下标i有关。首先将输入值Ei缓存中设置为长期有效的,也就是说其一直都是计算好的。在eCache中,代码nonzero(oS.eCache[:,0].A)[0]构建除了一个非零表。nonzero()返回了一个列表,这个列表包含以输入列表为目录的列表值,非零。nozero()语句返回的是非零E值所对应的alpha值,而不是E本身。程序会在所有值上进行循环并选择其中使得改变最大的那个值。如果这是第一个循环,那么就随机选择一个alpha值。当然,也有其他的方法。
程序清单的代码几乎和之前给出的smoSimple()的函数一模一样,但是这里的代码已经使用了自己的数据结构。这个结构在参数oS中传递。第二个重要的修改就是使用程序清单的selectJ来选择第二个alpha的值。最后在alpha值改变的时候更新Ecache。程序订单把上述过程打包在一起的代码片段。这就是选择第一个alpha值的外循环。
程序清单给出的是完整的Platt SMO算法,其输入和函数smoSimple()完全一样。函数一开始构建一个数据结构来容纳所有的数据,然后需要对控制函数退出的一些变量进行初始化。整个代码的主体是while循环,这与smoSimple()有些类似,但是这里的循环退出条件就更多一些。如果整个代码的主体是while循环,这与smoSimple()有些类似,但是哲理的循环条件退出条件就更多一些。当迭代次数超过指定的最大值,或者遍历整个集合都未对任何alpha值进行修改的时候,就退出循环。这里的maxIter变量和函数smoSimple()中的作用有一点不同,后者当没有任何alpha发生改变时会将整个集合的第一次遍历过程记成一次迭代,而这里的一次迭代定义为一次循环过程,而不论其做了什么事情。此时,如果在优化过程中存在波动就会停止,因此这里的做法优于smoSimple()函数中的计数方法。
while循环的内部与smoSimple()有所不同,一开始的for循环在数据集上遍历任何可能的alpha。我们通过调用innerL()来选择第二个alpha,并在可能时候对其进行优化处理,如果有任意一对alpha值发生改变,那么就会返回1.第二个for循环遍历所有的非边界alpha值,也就是不再边界0或者C上的值。
接下来,我们对for循环在非边界循环和完整遍历之间进行切换,并打印出迭代次数。最后程序将会返回常数b和alpha值。
然后可以得出下面的结果:
这样的结果更快。
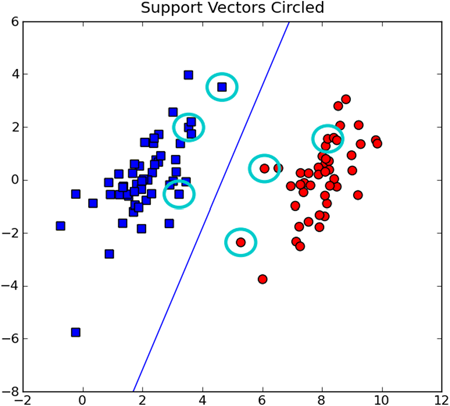
图中画圈的支持向量就给出了满足算法的一种解。如果数据集非线性可分,就会发现支持向量会在超平面附近聚集成团。
刚才我们花了大量的时间来计算alpha值,但是如何利用它们进行分类呢?这不成问题,首先必须基于alpha得到超平面,这也包括了w的计算。下面列出的一个小函数可以用于实现上述任务:
上述代码最重要的部分是for循环,虽然在循环中实现的只是多个数的乘积。前面计算出的任何一个alpha值,就不会忘记大部分alpha值为0.而非零alpha所对应的也就是支持向量。虽然上述for循环遍历了数据集中的所有数据,但是最终起作用的只有支持向量。由于对w计算毫无作用,所以数据中其他的数据点会被很容易舍弃。
为了使用前面给出的函数,输入下面的命令:
如果这个值大于0,则输入1类;如果这个值小于0,则属于-1类。对于数据点0,应该得到的类别标签是-1.可以通过如下的命令确定分类结果的正确性:
这样我们可以成功的训练出分类器了,但是如果两类数据点分别分布在一个圆的内外部,那么会的到怎么样的分类面呢?
在复杂数据上应用核函数
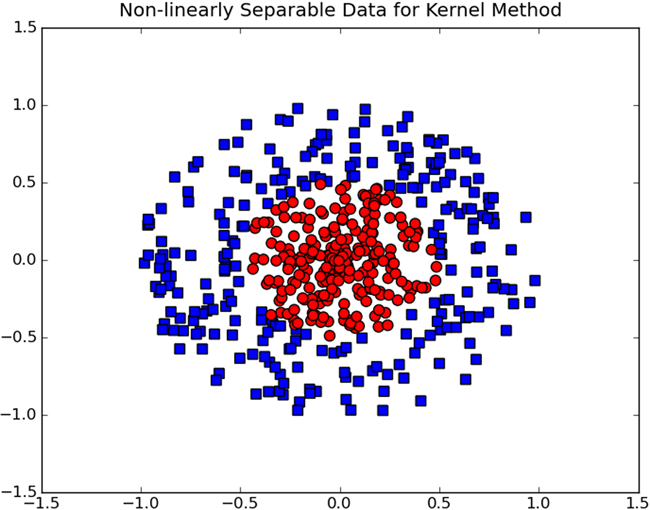
我们现在就需要使用一种成为核函数(kernel)的工具将数据转换成易于分类器理解的形式。首先解释核函数的概念,并且介绍它们在支持向量自动机的使用方法,然后我们介绍一种成为径向基函数(radial basis function)的最流行的核函数。最终将这个核函数应用与我们前面得到的分类器。
利用核函数将数据映射到高维空间
在上图中,数据点处于一个圆中,我们可以对圆中的数据进行转换,也就是把数据从一个特征空间转换到另一个特征空间,也就是一个映射。
从某个特征空间到另一个特征空间的映射会通过核函数来实现的,它能把数据从一个很难处理的形式转换成一个比较容易处理的形式,同时,核函数也有很多种类型,经过空间转换之后,我们就能够在高维空间解决线性问题,等价于在低维空间解决非线性问题。
SVM中,所有的运算都可以写成内积的形式,这样我们就可以把内积运算替换成核函数的形式。核函数不仅仅应用于支持向量自动机,很多其他机器学习算法也用到核函数。
径向基核函数
径向基函数是一个采用向量作为自变量的函数,能够基于向量距离运算输出一个标量。这个距离可以是从<0,0>向量或者其他向量开始计算的距离,其具体公式为:[k(x,y)=exp\left(\dfrac{-||x-y||^{2}}{2\sigma^{2}}\right)],其中[\sigma]是我们定义的用于确认函数跌落到0的速度参数。
上述高斯函数核函数将数据映射至高维空间(具体来说是一个无穷远的空间)。可以在已有代码中使用核函数。首先我们输入函数kernelTrans()。然后对optStruct类进行修改,得到核转换函数。
optStruct除了引入一个新变量kTup外,该版本和原来的optStruct一模一样。kTup是一个包含核函数信息的元祖,在初始化方法结束的时候,矩阵K先被构建,然后再通过调用函数kernelTrans()进行填充。全局K值只需要计算一次。当需要使用核函数的时候,就能过对他进行调用,也节省了很多的冗余的计算开销。
当计算矩阵K时,这个过程多次调用了kernelTrans()。这个过程有三个输入参数:2个数值型变量和1个元祖。元祖kTup给出的是核函数的信息。元祖的第一个参数是描述所用核函数类型的字符串,其他2个参数则都是核函数可能需要的可选参数。这个函数首先构建了一个列向量,然后检查元祖来确定核函数的类型。
在线性核函数的情况下,内积计算在“所有数据集”和“数据集中的一行”这两个输入间展开。在径向基函数的情况下,在for循环中对于矩阵的每个元素计算高斯函数的值。而在for循环结束之后,我们将计算过程应用到整个向量上去。
于是我们要对innerL和calcEk函数进行修改
测试中使用核函数
接下来我们将构建一个对数据点进行有效分类的分类器,这个分类器使用了径向基函数。前面提到基函数有一个用户定义的$\sigma$。首先我们需要确定其大小,然后利用该核函数构建出一个分类器。
上述代码只有一个可选的输入参数,这个输入参数是高斯径向基函数中的一个用户定义变量。整个代码主要是由以前定义的函数类型构成的。首先,程序从文件中读取输入数据集,然后在这些数据集上运行Platt SMO算法,其中核函数的类型为rbf。
整个代码最重要的就是for循环开始的两行,他们给出了如何利用核函数进行分类。首先利用结构初始化方法使用过的kernelTrans()函数,得到转换后的数据。然后,在使用之前的alpha以及类别标签求积。需要特别注意的是,在这几行代码中,是如何做到只需要支持向量数据就进行分类的。
与第一个for循环相比,第二个for循环仅仅只有数据集不同,后者采用的是测试数据集。可以输入下面的命令:
这个是结果
共有100个数据点,其中85个是支持向量,而当k从0.1变动到1.3的时候,支持向量少了很多,此时测试的错误率也在下降。该数据集在这个设置的某处存在最优值。如果降低了$\sigma$,那么训练错误率就会降低,但是测试错误率回升高。
支持向量的数目会存在一个最优值。SVM的优点在于他能够对数据进行高效分类。如果支持向量很少,那么就会得到一个很差的决策边界;如果支持向量很多,那么就相当于每次都利用整个数据集进行分类,这种方法成为k近邻。