前言
这篇文章主要来自于http://zkread.com/article/1130090.html,其参考的论文是MOSS的查重原理:http://theory.stanford.edu/~aiken/publications/papers/sigmod03.pdf。
winnowing算法
winnowing也就是筛除的意思,也就是说,我们需要从源代码之中直接删除掉无用的信息,提取出特征值来匹配。
k-gram模型
K-gram/ n-gram 英文翻译过来就叫做n元语法模型 参见维基百科: n-gram English version n-gram 中文版
k-gram 就是将一个连续的文本进行切割,每一个部分的长度都是k。当长度为1,2, 3时 分别对应的名称叫做 一元语法(1-gram unigram), 二元语法(bigram),三元语法(trigram).
为了形象的说明这个问题,我们来举一个简单的例子。有一个简单的文档 叫做A,由字母yabbadabbadoo组成:
这个时候我们在A这个文档上取一个大小为3的滑动窗口,就得到了一个3-gram 的集合:

A : yab abb bba dad ada dab abb bba bad ado doo
我们把这个集合中的元素都称为shingle.
下面我们再来看另一个文档C,文档C由下面的这些字符组成的:doobeedoobeedoo:
我们在为3构建一个3-gram 的集合,那么组成的shingle就是下面这个样子的:
C : doo oob obe bee eed edo doo oob obe bee eed edo doo
那么我们要比较A和C之间的相似性,我们很容易看出来我们只要比较他们的Shingle集合中相似的有多少就可以了。 在A和C集合中我们可以发现他们共有的元素是doo,但是他在A集合中出现了一次,在C集合中出现了三次。
那么这里就有两种可能,一种就是这是偶然的,还有一种假设就是万一真的存在剽窃呢,那就是说明doo 从A中被复制到C中三次。
但是其实这种情况,完全是取决与我们的K
看下面我们对A和C进行重新的划分,我们去k=4
A : yabb abba bbad bada adab dabb abba bbad dado adoo C : doob oobe obee beed eedo edoo doob oobe obee beed eedo edoo
可以看出现在这样子划分,这两个字符串是完全没有相似性可言的。
注意: 通过我们前面的观察,或者计算,对于一个含有N个字符的文档,我们按照k来划分得到的shingle 的个数是: N-K+1
K的选取
根据上面的分析我们知道,在这里最重要的就是选取K值。那么我们要怎么分割呢,一般我们文档的常见单词(不重要的出现频率大)的长度必须要小于 K.
注意注意重点来了!!!
我们选取的K必须大于文档中常见的不重要的单词,比如说在一个文档里,中文文档,最常见的单词应该是“的”,这个次几乎是每个文档都会出现的,但是这个次可能对于文档的相似性判断没有任何重要性而言。
又比如说我们英文当中的the 和我们程序当中的if 都是我们不太关心的,所以K的取值一般要比这些单词要大。这样就很好的剔除了文档中自然产生的相似性。
我们使用论文中的原话来讲,我们要查找一些我们感兴趣的信息,重要的shingle的长度必须要大于K,这些使我们感兴趣的,比K小的就是我们不敢兴趣的。你看,这是不是就是一个简单的过滤过程,首先通过K我们可以过滤掉一些信息。
k-gram 最有意思的特征就是,在某种程序上他对于排序是不敏感的。注意关键词, 某种程度上是不敏感的. 这样可以防止有的人重新排列了我们的文档,这种情况在代码中最为常见,比如说一个代码中有两个类,我们先后调换一下位置,这两份文档还是不能躲过我们k-gram hash 算法的火眼金睛。
比如说我们将 yabbadabbadoo 重新排列成 bbadooyabbada 混淆之后我们得到文档的shingle集合是: A: bba bad ado doo ooy oya yab abb bba bad ada
通过观察我们可以发现,3连字任然完整无缺的出现在其中,那么我们把这个文档和我们的C文档比较一下,他们的相似度是不变的。
hash算法
但是假设把这些信息都纳入计算,那么计算的开销无疑是巨大的。所以我们选择hash来直接提取特征值。
Hash 算法就是把任意长度的输入,通过散列算法,变换成固定长度的输出。该输出就是散列值。这种转换是一种压缩映射,散列值的空间一般远小于输入的空间。 但是如果不同的数据通过hash 算法得到了相同的输出,这个就叫做碰撞,因此不可能从散列值来唯一确定输入值。
一般的hash 算法我们都要求满足几个条件:
单向性(one-way), 从预映射,能够简单迅速的得到散列值,而在计算上不可能构造一个预映射,使其散列结果等于某个特定的散列值,即构造相应的M=H-1(h)不可行。这样,散列值就能在统计上唯一的表征输入值,因此,密码学上的 Hash 又被称为”消息摘要(messagedigest)”,就是要求能方便的将”消息”进行”摘要”,但在”摘要”中无法得到比”摘要”本身更多的关于”消息”的信息。
第二是抗冲突性(collision-resistant),即在统计上无法产生2个散列值相同的预映射。给定M,计算上 无法找到M’,满足H(M)=H(M’) ,此谓弱抗冲突性;计算上也难以寻找一对任意的M和M’,使满足H(M)=H(M’) ,此谓强抗冲突性。要求”强抗冲突性”主要是为了防范 所谓”生日攻击(birthdayattack)”,在一个10人的团 体中,你能找到和你生日相同的人的概率是2.4%,而在同一团体中,有2人生日相同的概率是11.7%。类似的, 当预映射的空间很大的情况下,算法必须有足够的强度来保证不能轻易找到”相同生日”的人。
第三是映射分布均匀性和差分分布均匀性,散列结果中,为 0 的 bit 和为 1 的 bit ,其总数应该大致 相等;输入中一个 bit的变化,散列结果中将有一半以上的 bit 改变,这又叫做”雪崩效应(avalanche effect)”; 要实现使散列结果中出现 1bit的变化,则输入中至少有一半以上的 bit 必须发生变化。其实质是必须使输入 中每一个 bit 的信息, 尽量均匀的反映到输出的每一个 bit上去;输出中的每一个 bit,都是输入中尽可能 多 bit 的信息一起作用的结果。
hash 算法最常用的就是加减乘除和移位运算。我们先来看几个常用常见的哈希函数吧。
观察上面的这些hash算法我们可以发现,输入都是一些字符串,我们需要对字符串进行操作,并且是对字符串的每一个位置上的字符串进行操作,移位加减乘除,等运算然后得到我们的散列置。在这里我们采用的hash 算法是下面这个:
[ c{1}*b^{k-1}+c{2}b^{k-2}+….+c_{k-1}b+c_{k} ]
其中H表示的是映射关系,这里操作的对象是我们的每一个shingle,所以C1…CK表示的是一个有K位的元model ,将每一个C按照我们的公式进行计算得到一个hash 值,这里的b 表示的是一个基底(Base) 这里是用户自己设定的某个值,我们一般选取一个质数来做我们的基底,按照上面的公式我们计算得到我们每个 Shingle的hash 值。
有了我们的hash算法,我们就可以计算每一个shingle的hash值。 我们的文档有N,按照k 来划分,得到的shingle 总共是N-K+1个。所以我们要计算N-K+1个长度为K的shingle的hash.
其实计算量还是很大的,不要着急,我们后面会讲怎么改进的,现在先卖个关子。
特征提取
什么是特征? 应该是能很快区分出你是谁的点,我们把这些你独一无二的东西叫做我们的“特”征。特征一定是能快速标记你是谁的东西。 在软件文本的检测中这个道理同样适用。
一个软件,它总有一些比较有价值的代码,和一些大众代码,我们谁都可以实现的。你有我有大家有的东西,显然不可能做特征。
我们在破案的时候,常常采用指纹,DNA,掌纹,牙齿的结构,等等来确定这个人是谁。我们没有必要比较所有的特征,因为那是没有任何效率的。比个DNA就能搞定的事情,你非要把身上的每一块肥肉都拿来判别一下,这个行为就是来搞笑的。
所以我们没有必要去比较一个文档的所有的shingle的hash值,我们只需要比较一些特定的hash 值,就可以了。这个时候就涉及到特征的提取和选择,到底那些特征是该保留的,那些特征是该舍弃的?
现在我们有一整个文档的hash 值,那有的人就说了,那我们每隔几个选一个hash 值带代替整个文档,让这些哈希值作为我们整个文档的“胎记”birthmark 或者是”指纹”fingerprint 也就是我们的特征。
OK,这个想法却是减小了我们的特征值,但是有效么?
我们思考一下.
随机每隔相通的距离选取一个hash值,这样的做法有什么弊端么?有可能这些哈希值全部都是不重要的信息的hash, 你用这些值根本找不到剽窃样本。
所以某种程度上效果不好。
之后又有人 提出了我们使用 θmodp = 0 的方法来选择我们的hash 值。这样又使得我们的选择更加的随机。
假设我们有一组hash 值,是这个样子的:
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 77 72 42 17 98 50 17 98 8 88 67 39 77 72 42 17 98
那我们选取 mod 4 =0 的哈希那我们就得到了 四个hash值做我们文档的特征值
我们得到的特征值就是: (1:72), ( 8:8), (9:88) , (13:72)
这个算法比上面的选取固定值又提升了一部,使得选取更加的随机化。但是,有问题么??
假设我们的散列值是下面这个排序:
72 8 88 72 77 42 17 98 50 17 98 67 39 77 42 17 98
那我们去p=4 ,我们取出来的hash值全部都来自头部的hash, 假设这个文章是有很多段组成的,我们这样选取,很可能使得我们的特征分布不均匀。这样我们很可能只提取到了某些段落的特征值,而完全的忽略了某些段落。
要是我们忽略的段落正好是我们抄袭的段落,那么我们很可能就完全检测不到了。所以,你可以看到这个方法的缺点了吧。有时候取余选取的特征值存在分配不均匀的情况。为了改善这个情况,我们就要推出我们今天的主角 winnowing.
Winnowing方法
为了使得我们的选取的特征值分布相对来说比较合理一点,这里我们使用了winnowing 的方法。在上面的一个小节中我们已经对这个方法做了一个简单的介绍。
这个方法的基本思想就是,我们首先设置一个大小为W的滑动窗口。将每个窗口中最小的那个hash保留下来(如果窗口中最小的hash 有两个或者多个,就保留最右边的那一个),这样就保证了我们保留下来的文档原文的间隔不会超过 W+K-1.注意,选过的特征是不能在挑选的,我们需要记录下下标。因为hash值是可能重复的。
为什么我们能保证间隔就是 W+K-1?why? 你想过这个问题了没有?
好的我们现在再来解答一下这个问题: 我们的特征值如下:
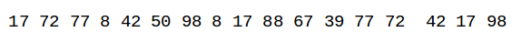
我们假设我们选取的窗口的大小为4:
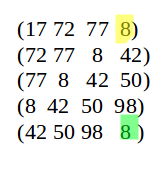
在第一个窗口中我们的最小值是A3:8,以此类推

在第二个窗口中我们的最小值依然是A3:8

在第三个窗口中我们的最小值依然是A3:8

在第四个窗口中我们的最小值依然是A3:8

直到第五个窗口的时候我们才能加入新的特征值

我们可以看到最差的情况就是上面我们说的这情况,其实就是W-1
按照这种方法我们可以选举出我们的所有特征值。
假设我们的hash值的集合是下面这个样子
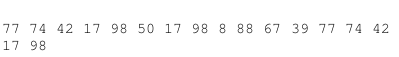
我们设置窗口的大小为4:

我们得到最终的特征值就是下面这个样子:

前面的是特征值,后面的是特征值对应的下标。