何谓CapsNet
在去年,Hinton提出了一个新的“胶囊”的概念来处理图像识别的问题,经过论文的证实,其取得了比CNN更好的效果。在这里,我简要的介绍一下关于CapsNet的内容。
为何提出了这个框架
在人类对于图像的识别中,往往我们会从图像中知道很多性质的实体。举例而言,位置、大小、方向、变形程度、速度、物件表面的反射率、气氛和纹理等都是我们识别图片的重要依赖。一个非常重要的特点就是在图像之中的实体,一个能显著表示其存在的方法就是使用一个逻辑单元,其输出的是这个实体是否存在的概率。在这个文章里面他们使用含有实体参数向量的总长度来表示实体的存在的概率(其不能大于100%,也就是1),而用其方向来表示实体的属性。
routing by agreement策略
这篇文章主要提出了一个强大的动态路由的规则使得“胶囊”在该层输出一个合适的亲本。
在起始阶段,CapsNet会输出所有可能的亲本,但是输出会被亲本的系数所重置,其系数的和为1。对于没一个可能的亲本,Capsule将会通过把它的输出和一个权重矩阵相乘计算出一个预测的矢量。如果这个预测的矢量比某一个可能的亲本的输出还要大的话,一个从上到下的反馈就会启动。这个反馈将会增大对应亲本的系数并且减小其他亲本的输出。这个策略将会比原始形式的max-pooling(最大池化)更有效率,池化使得在一个层里的神经元只会关注到最活跃的特征而舍弃其他的特征。在针对高度重叠的物件的分割之中,这种新的策略能够非常有效地执行“解释(原文是explaining away)”的作用。
卷积神经网络使用已经学习过特征的解释的副本来工作,其允许他们在图片中某个位置利用合适的权值来工作,这也在图像识别中被证实非常有用。尽管我们用使用routing-by-agreement的矢量输出胶囊和最大池化的方法来取代标量输出的CNN,我们仍然希望知道数据在空间的分布。所以我们将会把除了最后一层的胶囊层都使用卷积的方法。在CNN的协助下,我们将会使用高层的胶囊来处理更大面积上的图像。与最大池化的方法不一样,我们并不会丢失任何关于实体处于区域之中的精确位置信息。对于低维的胶囊来说,未知的信息将会被活跃的胶囊所编码。当我们升序按照等级排序的时候,越来越多的位置信息将会被胶囊输出的矢量的实值所“rate-coded”(率编码)。这种由对位置编码到率编码的转变伴随着高层的胶囊在更大自由度上能表达更复杂的实体信息。也就是说,胶囊的维度随着我们增加等级的同时,其也随之上升。
矢量的胶囊输入和输出是如何被计算的
其主要的是,胶囊的输出矢量长度代表着实体的可能性。我们因此就是用一个非线性的“压扁”函数来确保短的矢量长度压到接近于0而长矢量的长度压缩到接近于1。
$$ v_j = \frac{||s_j||^2}{1+||s_j||^{2}} \frac{s_j}{||s_j||} $$
$ v_{j} $ 就是第 $ j $ 个胶囊的矢量输出,$ s_{j} $ 是总体的输入
对于除了第一个层的胶囊来说,一个$ s_{j} $的胶囊的总体的输入是一个对于预测矢量的加权和,也就是
$$ s_{j} = \sum_{i} c_{ij} \hat{u}_{j|i} $$
$$ \hat{u}_{j|i} = W_{ij}u_{i} $$
$ c_{ij} $是动态路由过程之中的参数。
在胶囊$ i $ 和所有胶囊层的系数相加的和为1并且其也会被“routing softmax”所决定的。而其初始值$ b_{ij} $就是对数的先验概率,$ i $和$ j $的胶囊的匹配的系数应该就是
$$ c_{ij} = \frac{exp(b_{ij})}{\sum_{k}exp(b_{ik})} $$
这个对数的先验概率可以因为对称性取得其他的权重。他们仅仅取决于位置和胶囊的类型,其不依赖于现有的输入的图像。初始的系数对接下来就被通过衡量现有的输出$ v_j $ 和是由j层第i个胶囊给出的预测值 $ \hat{u}_{j|i} $来迭代刷新值.
相似度的值可以通过 $ a_{ij} = v_{j} \hat{u}_{j|i} $ 。当其是一个对数的相似值并且被加到初始的逻辑单元的时候,这个相似值就会被处理。在在计算将胶囊$ i $连接到更高级别胶囊的所有相关系数的新值之前。
在卷积的胶囊层里面,没一个胶囊都会输出一个胶囊在本地网格的矢量。对于每个网格和胶囊,其都会使用不同的变换的方式。
下面就是路由的算法:
|
|
边缘分布
Capsule使用一个矢量来表达胶囊实体存在的可能性。对于最顶层的胶囊来说,当且仅当这一位在图片中出现的时候,对应的第k类将会有一个长的实例化向量。为了其能够适用于不同的类,对于每一个类所对应的胶囊,我们将会使用一个单独的边缘分布$L_{k}$:
$$ L_{k} = T_{k} \max(0,m^{+}-||v_{k}||)^{2} + \lambda (1-T_{k}) \max(0,||v_{k}||-m^{-})^2 $$
若存在k类的数字,则$ T_{k} = 1 $,与此同时$ m^{+} = 0.9 $ ,$ m^{-} = 0.1 $。损失的$ \lambda $降权重将会针对其他无关的类,最初从缩短所有胶囊的矢量的长度中学习的情况也会被终止。这里我们使用$ \lambda = 0.5 $。总的损失就仅仅是其他胶囊的损失的和。
CapsNet架构
一个简单的CapsNet如图所示,这个架构如此的浅以至于只有两层卷积层和一层全连接层。Conv1是256维,9*9的卷积核,其步长为1和一个Relu激活函数。这个层能够将像素强度转换为特征检测的活动,并且将其作为初级胶囊的输入。
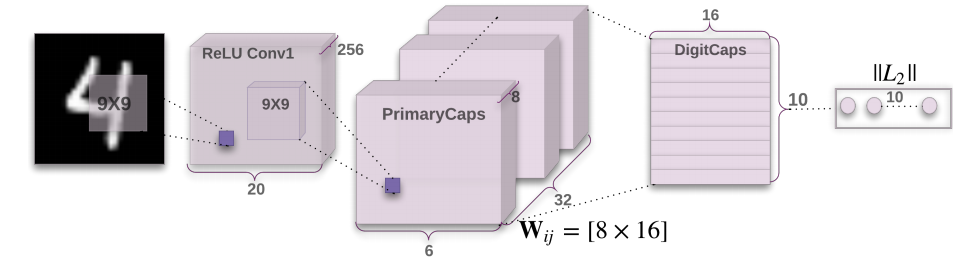
初级胶囊也就是多维实体的最低层,从图像反序列化的角度上来说,初级胶囊对应着反序列化的渲染过程。这比起拼凑实体来组成整体来说,胶囊和他们的工作的方式大不相同。
第二层也是一个卷积胶囊层,其是一个带有32个通道的8维的胶囊。每一个初级胶囊的输出和所有的256*81的卷积单元的输出是一致的。总体的初级胶囊有一个32*6*6的胶囊输出(每一个输出都是一个8维的矢量),每个处于6*6网格中的胶囊共享器权值。对于每一个类,最后的层对应着一个16维的胶囊。
这篇论文始终都只是针对两层胶囊层。因为conv1的输出都是一维的,所以自然也没有表达空间方向的空间。因此,在conv1和初级胶囊层之间自然也没有路由关系了。斯普皮的路由单元$b_{ij}$也初始化为0,因此,在初始阶段下,一个胶囊的输出就会被以等概率传递到所有亲本的胶囊层。在文章之中他也给出了一个tensorfloww的代码实现,并且使用了Adam优化器。
基于正则化的空间信息重建
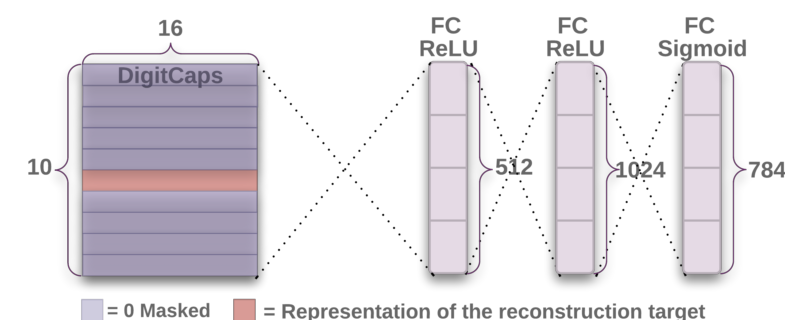
我们会使用一个附加的重建损失来让胶囊编码输入数字的实体参数。在训练过程中,我们将会对所有非正确数字的胶囊进行掩码。接下来我们就会使用这个活跃的矢量来重建输入图像。接着数字的胶囊的输出将会被送入一个包含3个全连接层的解码器,这个结构就如图2所示。我们会按照MSE的误差来优化网络。同时我们将会按照0.0005的倍数缩小重建误差,这样在训练的时候其就不会影响到边缘误差。论文中阐释了重建能够很好的还原重要的细节内容。

| 方式 | 路由次数 | 是否重建 | MNIST(%) | Multi-MNIST(%) |
|---|---|---|---|---|
| Baseline | - | - | 0.39 | 8.1 |
| CapsNet | 1 | no | 0.34+-0.0032 | - |
| CapsNet | 1 | yes | 0.29+-0.011 | 7.5 |
| CapsNet | 3 | no | 0.35+-0.036 | - |
| CapsNet | 3 | yes | 0.25+-0.005 | 5.2 |
Capsule 在MNIST数据集上的表现
在28*28的MNIST数据下,数据首先被在每个方向以0填充两个像素的策略所处理。这样的话训练集和验证集分别有6w和1w。