什么是迁移学习

迁移学习的研究来源于一个观测：人类可以将以前学到的知识应用于解决新的问题，从而提高解决问题的效率或取得更好的效果。因此迁移学习被赋予这样一个任务：从以前的任务当中去学习知识（knowledge）或经验，并应用于新的任务当中。换句话说，迁移学习的目的是从一个或多个源任务（source tasks）中抽取知识、经验，然后应用于一个有相关性的目标领域（target domain）中去。[1] 顾名思义就是就是把已学训练好的模型参数迁移到新的模型来帮助新模型训练。考虑到大部分数据或任务是存在相关性的，所以通过迁移学习我们可以将已经学到的模型参数（也可理解为模型学到的知识）通过某种方式来分享给新模型从而加快并优化模型的学习效率不用像大多数网络那样从零学习（starting from scratch，tabula rasa）。这里迁移学习通过Source / Target Domain Label就可以更为细节的分支为下面的几个方向

Transfer Learning Setting（迁移学习设定）	相关领域	源空间标签是否存在	目标空间标签是否存在	任务
Inductive transfer learning(归纳迁移学习)	多任务学习	存在	存在	回归或者分类
Inductive transfer learning(归纳迁移学习)	自我启发式学习	不存在	存在	回归或者分类
Transductive transfer learning(归纳迁移学习)	空间自适应，采样偏差，边缘分布变换	存在	不存在	回归或者分类
Unsupervised transfer learning(无监督迁移学习)		不存在	不存在	聚类或者降维

数学定义

假定现在有一个源空间 $ D_S = {X_S,f_S(X)} $和一个学习任务$ T_s $，一个目标空间$ D_T = {X_T,f_T(X)} $以及一个学习任务 $ T_T $，迁移学习目的是帮助依据$ D_S $和$ T_S $的知识，在$ D_T $域内的求得目标预测函数$ f_T(X) $，其中$ D_S\neq D_T$或者$ T_S\neq T_T$ .

在 inductive 的迁移学习里，我们有 Target Domain 的 Ground Truth Label，这就意味着我们想要迁移的数据所在 Domain 将直接会学习网络和其特征提供指导作用（假设用深度学习方法，则通过Back-progagation方式）。

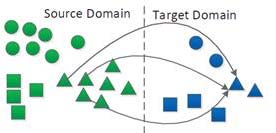
理论上，任何领域之间都可以做迁移学习。但是，如果源域和目标域之间相似度不够，迁移结果并不会理想，出现所谓的负迁移情况。比如，一个人会骑自行车，就可以类比学电动车；但是如果类比着学开汽车，那就有点天方夜谭了。如何找到相似度尽可能高的源域和目标域，是整个迁移过程最重要的前提。

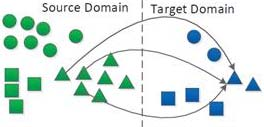
领域自适应问题

也就是Domain Adaptation，同构迁移学习，其具有下面的基本假设：

数据分布的角度：源域和目标域的概率分布相似（最小化概率分布距离）
特征选择的角度：源域和目标域共享某些特征（选择出公共特征）
特征变化的角度：源域和目标域共享某些子空间（把两个域变换到相同的子空间）

概率分布适配

边缘分布适配（Marginal distribution adaptation）
- 假设: $ P(X_S) \neq P(X_t) $
条件分布适配（Conditional distribution adaptation）
- 假设: $ P(y_S | X_S) \neq P(y_t | X_t) $
联合分布适配（Joint distribution adaptation）
- 假设: $ P(X_S,y_S) \neq P(X_t,y_t) $

边缘分布适配

迁移成分分析（Transfer Component Analysis），其优化目标为$$ min Dist(\varphi (X_S),\varphi(X_T)) + \lambda \Omega(\lambda) $$

$$ s.t. constraints~on~\varphi(X_S) and \varphi(X_T) $$

最大均值差异（Maximum Mean Discrepancy） $$ Dist(P(X_S),P(X_T)) = ||\frac{1}{n_S} \sum_{i=1}^{n_S} \Phi (x_{S_{i}}) - \frac{1}{n_T} \sum_{j=1}^{n_T} \Phi(x_{S_{j}})||_{H} $$

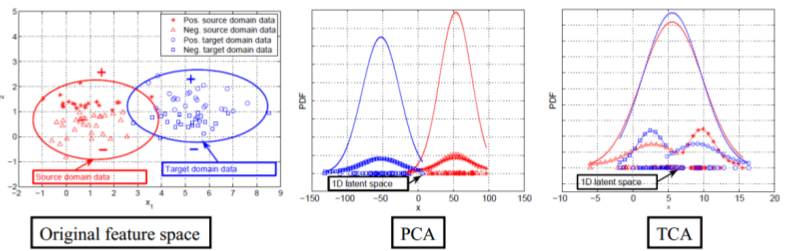
迁移成分分析（TCA）的扩展
- Adaptating Component Analysis（ACA）$ max~\dfrac{tr(HK_{X}HL_{\Phi})}{tr(HK_{M}HL_{\Phi})} $ 也就是最小化MMD，同时维持迁移过程之中目标域的结构
- Domain Transfer Multiple Kernel Learning 多核MMD
- Deep Domain Confusion 把MMD加入到神经网络中
- Deep Adaptation Network（DAN）把MKK-MMD加入到神经网络之中
- Distribution-Matching Embledding（DME）先计算变换矩阵，在进行映射
- Central Moment Discrepancy（CMD）k阶MMD

条件分布适配

Domain Adaptation of Conditional Probability Models via Feature Subsetting

主要就是条件随机场和分布适配，其优化目标为: $$argmax_{w,s}~ \sum_{(x,y)\in D}\sum_{k\in S} \omega_k f_k(x,y) - \log z_w(x) $$
$$ such~that~dist(D,D’|S,D’) \leq \epsilon$$

Conditional Transferrable Components (CTC)

定义条件转移成分,对其进行建模

联合分布适配

直接继承于TCA，但是加入了条件分布适配，其优化目标为$ D(D_s,D_t) \approx D(P(x_s),P(x_t)) + D(P(y_s|x_s),P(y_t|x_t)) $

这样我们可以使用一个充分统计量，也就是类条件概率近似条件概率，也就是用一个弱分类器生成目标域的初始软标签，所以最终的优化形式为$ \min_{A^TKHK^TA = I} \sum_{c=0}^{C} tr(A^TKM_cK^TA) + \lambda||A||^2_{F} $

联合分布适配的结果普遍优于单独适配边缘或者条件分布

联合分布适配方法的一些扩展：

Adaptation Regularization（ARTL）分类器学习+联合分布适配
Visual Domain Adaptation（VDA）加入类间距、类内距
Joint Geometrical and Statistical Alignment（JGSA）加入类间距、类内距和标签适配
或者加入结构不变性控制
目标域选择
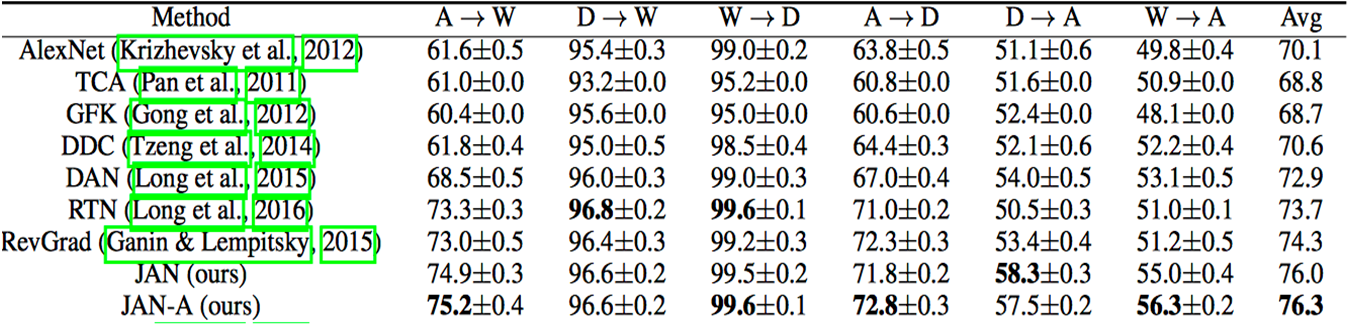
Joint Adaptation Network（JAN）提出JMMD度量，在深度网络中进行联合分布适配

在这里，还有一类非常重要的，联合分布适配（Balanced Distribution Adaptation, BDA），这里使用平衡因子来动态衡量两种分布的重要性，也就是$ D(D_s,D_t) \approx (1-\mu)D(P(x_s),P(x_t)) + \mu D(P(y_s|x_s),P(y_t|x_t)) ~ \mu \in [0,1] $

当$ \mu \rightarrow 0 $，表示边缘分布更占优，应该优先适配
当$ \mu \rightarrow 1 $，表示条件分布更占优，应该优先适配

最终表达形式为：$$ min~ tr(A^TX((1-\mu)M_0+\mu \sum_{c=1}^{C}M_c)X^TA) + \lambda ||A||^2_F $$
$$ s.t.~ A^TXHX^TA = I, ~0\leq \mu \leq 1 $$

平衡银子的重要性在于：对于不同的任务，边缘分布和条件分布并不是同等重要，因此，BDA方法可以有效衡量这两个分布的权重，从而达到最好的结果。

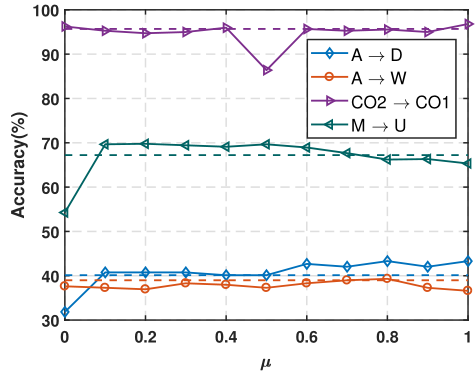
平衡银子的求解和估计来说，目前没有精确估计方法，我们一般使用A距离来进行估计

求解源域和目标域整体的A距离
对目标域聚类，计算源域和目标域每个类的A距离
计算上述两个距离的比值，也就是平衡因子

总结

大部分方法都是基于MMD距离进行优化求解，然后可以分别进行边缘/条件/联合概率适配，在效果上，平衡 (BDA) > 联合 (JDA) > 边缘 (TCA) > 条件。

数据整体差异性大 (相似度较低),边缘分布更重要
数据整体差异性小 (协方差漂移),条件分布更重要

使用深度学习和分布适配往往有更好的效果。

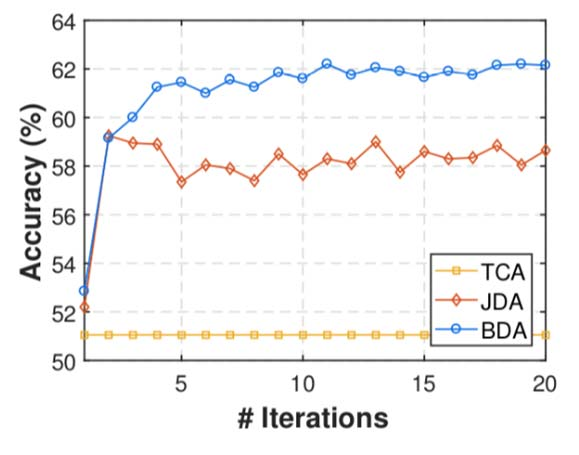
特征选择法

从源域和目标域中选择提取共享的特征,建立统一模型，寻找Pivot feature,将源域和目标域进行对齐。
特征选择法

扩展有：

Joint feature selection and subspace learning 特征选择/变换+子空间学习
- 优化目标:$$ min_A ||A||_{2,1} + \mu tr(A^TXLX^TA), s.t. A^TXDX^TA = I $$
Transfer Joint Matching (TJM) MMD分布适配+源域样本选择
- 优化目标: $$ \min_{A^TKHK^TA = I} tr(A^TKHK^TA)+\mu (||A_s||_{2,1}+||A_t||_F^2) $$
Feature Selection and Structure Preservation (FSSL) 特征选择+信息不变性
- 优化目标:$$ \min_{P,Z,E} ||P||_{2,1} + \frac{\mu}{2} tr(P^TXLX^TP) + \frac{\beta}{2} ||Z||^2_F + \gamma ||E||_1 ,~~ s.t. P^TX_sZ+E, P^TXDX^TP = I$$

其特点有：

从源域和目标域中选择提取共享的特征,建立统一模型
通常与分布适配进行结合
选择特征通常利用稀疏矩阵

子空间学习法

将源域和目标域变换到相同的子空间,然后建立统一的模型

统计特征变换 (Statistical Feature Transformation)
- 将源域和目标域的一些统计特征进行变换对齐
流形学习 (Manifold Learning)
- 在流形空间中进行子空间变换

统计特征变换

子空间对齐法 (Subspace Alignment, SA)

直接寻求一个线性变换,把source变换到target空间中
优化目标: $$ F(M) = ||X_SM-X_T||^2_F $$ $$ M^* = argmin_M(F(M)) $$
直接获得线性变换的闭式解: $$ F(M) = ||X_S’X_SM-X_S’X_T||^2_F = ||M-X_S’X_T||^2_F $$

子空间对齐+概率分布适配 $$ M_s = S_sT_TA_TS_t^T = S(S^TS)(E_s^{-\frac{1}{2}}E_t^{\frac{1}{2}})S^T $$

关联对齐法 (CORrelation Alignment, CORAL)

最小化源域和目标域的二阶统计特征，其优化目标为：$ \min_{A} = ||C_S - C_T||^2_F = \min_{A}||A^TC_sA-C_T||^2_F $
形式简单，求解高效

深度关联对齐 (Deep-CORAL)

深度学习之中加入CORAL，$ CORAL = \frac{1}{4d^2}||C_S-C_T||^2_F $

流形学习

采样测地线留方法（Sample Geodesic Flow）

把领域自适应的问题看成一个增量式“行走”问题
从源域走到目标域就完成了一个自适应过程
在流形空间中采样有限个点,构建一个测地线流

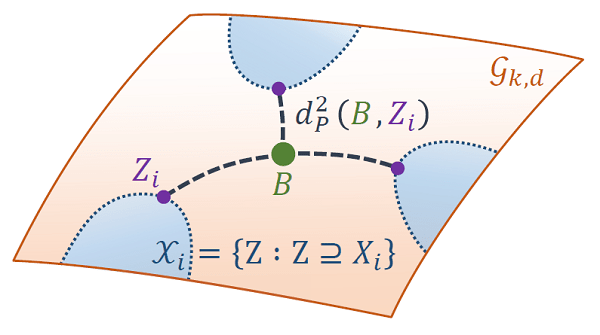
测地线流式核方法 (Geodesic Flow Kernel, GFK)

继承了SGF方法,采样无穷个点
转化成Grassmann流形中的核学习,构建了GFK
优化目标:$ (z_i^\infty,z_j^\infty) = \int_0^1 (\Phi(t)^Tx_i)^T (\Phi(t)^Tx_j)^T dt = x_i^TGx_j $

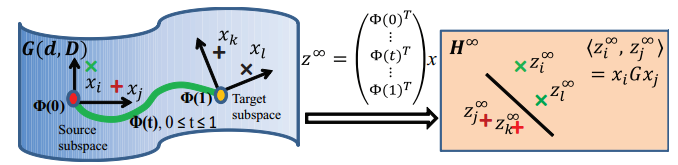
域不变映射 (Domain-Invariant Projection, DIP) [Baktashmotlagh,CVPR-13]

直接度量分布距离是不好的:原始空间特征扭曲
仅作流形子空间学习:无法刻画分布距离
解决方案:流形映射+分布度量

统计流形法 (Statistical Manifold) [Baktashmotlagh, CVPR-14]

在统计流形(黎曼流形)上进行分布度量
用Fisher-Rao distance (Hellinger distance)进行度量

$$ \min_\alpha = \dfrac{1}{\sum_{i=1}^{n_s}\alpha_i} \sum_{i=1}^{n_s} \alpha_i (\sqrt{T(x_i^s)}- \sqrt{1-T(x_i^s)} )^2 + \dfrac{1}{n_t} \sum_{i=1}^{n_s} (\sqrt{T(x_i^s)}- \sqrt{1-T(x_i^s)})^2 $$

总结

主要包括统计特征对齐和流形学习方法两大类
和分布适配结合效果更好
趋势:与神经网络结合

某不科学的kidozh

迁移学习初步